Question Number 176501 by infinityaction last updated on 20/Sep/22
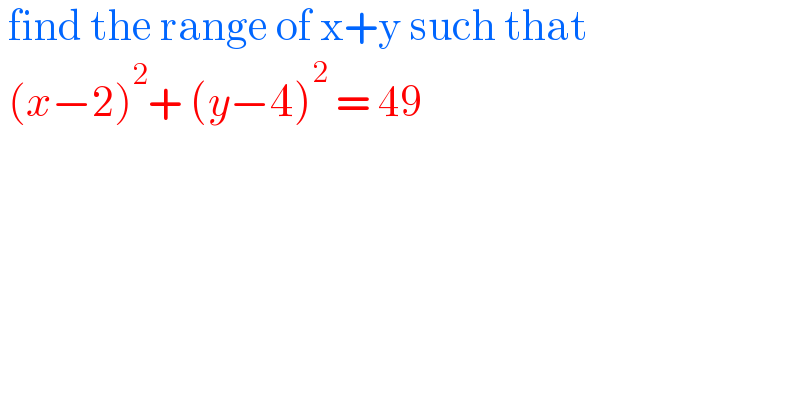
$$\:\mathrm{find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{x}+\mathrm{y}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\:\left({y}−\mathrm{4}\right)^{\mathrm{2}} \:=\:\mathrm{49} \\ $$
Commented by cortano1 last updated on 20/Sep/22
![let x+y=k ⇒x+y−k=0 is tangent to circle so 7=((∣2+4−k∣)/( (√2))) ⇒∣k−6∣ = 7(√2) ⇒−7(√2) ≤ k−6≤7(√2) ⇒6−7(√2) ≤k≤6+7(√2) Therefore range of x+y is [ 6−7(√2) , 6+7(√2) ]](https://www.tinkutara.com/question/Q176504.png)
$$\:\mathrm{let}\:\mathrm{x}+\mathrm{y}=\mathrm{k}\:\Rightarrow\mathrm{x}+\mathrm{y}−\mathrm{k}=\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{tangent}\:\mathrm{to}\:\mathrm{circle}\: \\ $$$$\mathrm{so}\:\mathrm{7}=\frac{\mid\mathrm{2}+\mathrm{4}−\mathrm{k}\mid}{\:\sqrt{\mathrm{2}}}\: \\ $$$$\Rightarrow\mid\mathrm{k}−\mathrm{6}\mid\:=\:\mathrm{7}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow−\mathrm{7}\sqrt{\mathrm{2}}\:\leqslant\:\mathrm{k}−\mathrm{6}\leqslant\mathrm{7}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{6}−\mathrm{7}\sqrt{\mathrm{2}}\:\leqslant\mathrm{k}\leqslant\mathrm{6}+\mathrm{7}\sqrt{\mathrm{2}} \\ $$$$\mathrm{Therefore}\:\mathrm{range}\:\mathrm{of}\:\mathrm{x}+\mathrm{y} \\ $$$$\mathrm{is}\:\left[\:\mathrm{6}−\mathrm{7}\sqrt{\mathrm{2}}\:,\:\mathrm{6}+\mathrm{7}\sqrt{\mathrm{2}}\:\right]\: \\ $$
Answered by Peace last updated on 20/Sep/22
![{ ((x=2+7cos(t))),((y=4+7sin(t))) :}t∈[0,2π[ x+y=6+7(sin(t)+cos(t))=6+7(√2)(sin(t+(π/4))) x+y∈[6−7(√2),6+7(√2)]](https://www.tinkutara.com/question/Q176529.png)
$$\begin{cases}{{x}=\mathrm{2}+\mathrm{7}{cos}\left({t}\right)}\\{{y}=\mathrm{4}+\mathrm{7}{sin}\left({t}\right)}\end{cases}{t}\in\left[\mathrm{0},\mathrm{2}\pi\left[\right.\right. \\ $$$${x}+{y}=\mathrm{6}+\mathrm{7}\left({sin}\left({t}\right)+{cos}\left({t}\right)\right)=\mathrm{6}+\mathrm{7}\sqrt{\mathrm{2}}\left({sin}\left({t}+\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$${x}+{y}\in\left[\mathrm{6}−\mathrm{7}\sqrt{\mathrm{2}},\mathrm{6}+\mathrm{7}\sqrt{\mathrm{2}}\right] \\ $$
