Question Number 176679 by mnjuly1970 last updated on 24/Sep/22
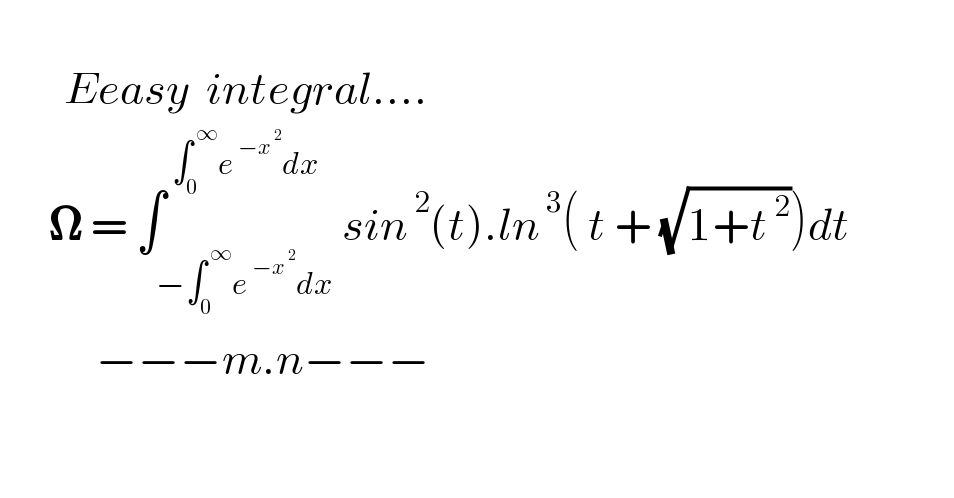
$$ \\ $$$$\:\:\:\:\:\:\:\:{Eeasy}\:\:{integral}…. \\ $$$$\:\:\:\:\:\:\boldsymbol{\Omega}\:=\:\int_{β\int_{\mathrm{0}} ^{\:\infty} {e}^{\:β{x}^{\:\mathrm{2}} } {dx}} ^{\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:β{x}^{\:\mathrm{2}} } {dx}} {sin}^{\:\mathrm{2}} \left({t}\right).{ln}^{\:\mathrm{3}} \left(\:{t}\:+\:\sqrt{\mathrm{1}+{t}^{\:\mathrm{2}} }\right){dt}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:βββ{m}.{n}βββ \\ $$
Answered by Peace last updated on 24/Sep/22
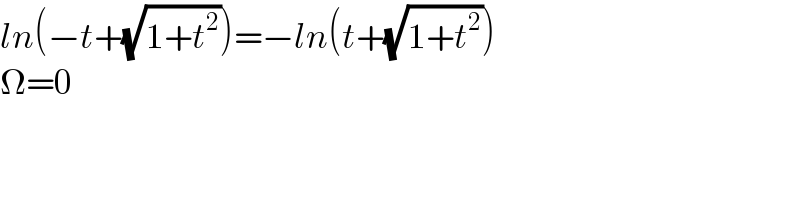
$${ln}\left(β{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)=β{ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$\Omega=\mathrm{0} \\ $$
Answered by mahdipoor last updated on 25/Sep/22
![βf(a)=β[sin^2 (a).ln^3 (a+(β(a^2 +1)))]= sin^2 (a).[βln(a+(β(a^2 +1)))]^3 = sin^2 (a).ln^3 ((1/(a+(β(a^2 +1)))))= sin^2 (a).ln^3 (((βa+(β(a^2 +1)))/([a+(β(a^2 +1))][βa+(β(a^2 +1))])))= sin^2 (βa).ln^3 (βa+(β((βa)^2 +1)))=f(βa) ββ βa , f(ΞΎ).Ξ΄x+f(βΞΎ).Ξ΄x=0 ββ get β«_0 ^β e^(βx^2 ) dx=m ΞΎ_i =i.Ξ΄x ββ 0=lim_(Ξ΄xβ0) Ξ£_(i=0) ^(m/Ξ΄x) f(βΞΎ_i ).Ξ΄x+f(ΞΎ_i ).Ξ΄x= lim_(Ξ΄xβ0) Ξ£_(βm/Ξ΄x) ^(m/Ξ΄x) f(ΞΎ_i ).Ξ΄x=β«_( βm) ^( m) f(x)dx](https://www.tinkutara.com/question/Q176707.png)
$$β{f}\left({a}\right)=β\left[{sin}^{\mathrm{2}} \left({a}\right).{ln}^{\mathrm{3}} \left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\right)\right]= \\ $$$${sin}^{\mathrm{2}} \left({a}\right).\left[β{ln}\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\right)\right]^{\mathrm{3}} = \\ $$$${sin}^{\mathrm{2}} \left({a}\right).{ln}^{\mathrm{3}} \left(\frac{\mathrm{1}}{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}\right)= \\ $$$${sin}^{\mathrm{2}} \left({a}\right).{ln}^{\mathrm{3}} \left(\frac{β{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}{\left[{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\right]\left[β{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\right]}\right)= \\ $$$${sin}^{\mathrm{2}} \left(β{a}\right).{ln}^{\mathrm{3}} \left(β{a}+\sqrt{\left(β{a}\right)^{\mathrm{2}} +\mathrm{1}}\right)={f}\left(β{a}\right) \\ $$$$\Rightarrow\Rightarrow \\ $$$$\forall{a}\:,\:\:{f}\left(\xi\right).\delta{x}+{f}\left(β\xi\right).\delta{x}=\mathrm{0} \\ $$$$\Rightarrow\Rightarrow \\ $$$${get}\:\int_{\mathrm{0}} ^{\infty} {e}^{β{x}^{\mathrm{2}} } {dx}={m} \\ $$$$\xi_{{i}} ={i}.\delta{x} \\ $$$$\Rightarrow\Rightarrow \\ $$$$\mathrm{0}=\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\underset{{i}=\mathrm{0}} {\overset{{m}/\delta{x}} {\sum}}{f}\left(β\xi_{{i}} \right).\delta{x}+{f}\left(\xi_{{i}} \right).\delta{x}= \\ $$$$\underset{\delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\underset{β{m}/\delta{x}} {\overset{{m}/\delta{x}} {\sum}}{f}\left(\xi_{{i}} \right).\delta{x}=\int_{\:β{m}} ^{\:{m}} {f}\left({x}\right){dx} \\ $$$$ \\ $$