Question Number 111882 by bemath last updated on 05/Sep/20
![(√(bemath)) (1)lim_(x→∞) [(x^2 /(x+1)) − (x^2 /(x+3)) ] ? (2) prove that n^2 ≤ 2^n for ∀n∈N by mathematical induction](https://www.tinkutara.com/question/Q111882.png)
$$\:\:\sqrt{{bemath}} \\ $$$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{x}^{\mathrm{2}} }{{x}+\mathrm{1}}\:−\:\frac{{x}^{\mathrm{2}} }{{x}+\mathrm{3}}\:\right]\:? \\ $$$$\left(\mathrm{2}\right)\:{prove}\:{that}\:{n}^{\mathrm{2}} \:\leqslant\:\mathrm{2}^{{n}} \:{for}\:\forall{n}\in\mathbb{N} \\ $$$${by}\:{mathematical}\:{induction} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Sep/20
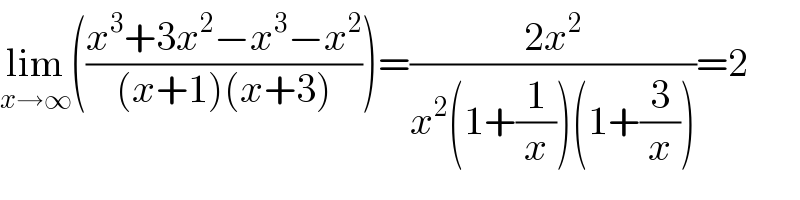
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} −{x}^{\mathrm{2}} }{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{3}}{{x}}\right)}=\mathrm{2} \\ $$
