Question Number 112179 by ajfour last updated on 06/Sep/20
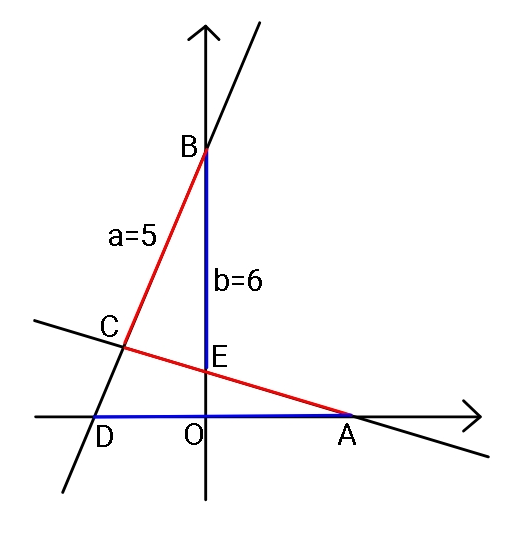
Commented by ajfour last updated on 06/Sep/20

$${If}\:{AC}={BC}=\:{a}=\mathrm{5} \\ $$$$\&\:\:\:{AD}={BE}={b}=\mathrm{6} \\ $$$${find}\:{equation}\:{of}\:{lines}\:{AC}\:{and}\:{BC}. \\ $$
Answered by mr W last updated on 06/Sep/20

Commented by mr W last updated on 06/Sep/20
![OD=b−p CE=a−(√(p^2 +q^2 )) a^2 =(a−(√(p^2 +q^2 )))^2 +b^2 −2b(a−(√(p^2 +q^2 )))(q/( (√(p^2 +q^2 )))) ⇒(a−(√(p^2 +q^2 )))(a−(√(p^2 +q^2 ))−((2bq)/( (√(p^2 +q^2 )))))=a^2 −b^2 ..(i) tan ∠B=((b−p)/(b+q)) cos ∠B=((a^2 +b^2 −(a−(√(p^2 +q^2 )))^2 )/(2ab)) 1+(((b−p)/(b+q)))^2 =((4a^2 b^2 )/([a^2 +b^2 −(a−(√(p^2 +q^2 )))^2 ]^2 )) (√(1+(((b−p)/(b+q)))^2 ))[a^2 +b^2 −(a−(√(p^2 +q^2 )))^2 ]=2ab ..(ii) p≈1.40282 q≈0.93054](https://www.tinkutara.com/question/Q112230.png)
$${OD}={b}−{p} \\ $$$${CE}={a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} =\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)\frac{{q}}{\:\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }} \\ $$$$\Rightarrow\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }−\frac{\mathrm{2}{bq}}{\:\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \:..\left({i}\right) \\ $$$$\mathrm{tan}\:\angle{B}=\frac{{b}−{p}}{{b}+{q}} \\ $$$$\mathrm{cos}\:\angle{B}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\mathrm{1}+\left(\frac{{b}−{p}}{{b}+{q}}\right)^{\mathrm{2}} =\frac{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{1}+\left(\frac{{b}−{p}}{{b}+{q}}\right)^{\mathrm{2}} }\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left({a}−\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)^{\mathrm{2}} \right]=\mathrm{2}{ab}\:\:\:..\left({ii}\right) \\ $$$$ \\ $$$${p}\approx\mathrm{1}.\mathrm{40282} \\ $$$${q}\approx\mathrm{0}.\mathrm{93054} \\ $$
Commented by ajfour last updated on 08/Sep/20

$${thanks}\:{for}\:{solving},\:{sir};\:{but}\:{i}\:{believe} \\ $$$${exact}\:{answer}\:{might}\:{be}\:{possible} \\ $$$${someway}.. \\ $$$${Just}\:{now},\:{i}\:{could}\:{prove}\:{that} \\ $$$${either}\:\angle{A}=\angle{B}\:\:{or}\:\:\angle{A}=\frac{\pi}{\mathrm{2}}+\angle{B} \\ $$$${we}\:{take}\:{the}\:{first}\:{case}\:{here}: \\ $$$$\Rightarrow\:{lines}\:{are}\:{perpendicular} \\ $$$${Then}\:\:\:{p}=\frac{{a}}{{b}}\left({a}−\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right) \\ $$$${and}\:\:\:\:\:\:{q}=\frac{\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{b}}\left({a}−\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right) \\ $$$${and}\:{for}\:\:{a}=\mathrm{5},\:{b}=\mathrm{6} \\ $$$$\:\:\:\:\:{p}=\frac{\mathrm{5}}{\mathrm{6}}\left(\mathrm{5}−\sqrt{\mathrm{11}}\right)\approx\:\mathrm{1}.\mathrm{4028} \\ $$$$\:\:\:\:\:{q}=\frac{\sqrt{\mathrm{11}}}{\mathrm{6}}\left(\mathrm{5}−\sqrt{\mathrm{11}}\right)\approx\:\mathrm{0}.\mathrm{9305} \\ $$$$\left({same}\:{as}\:{your}\:{answer}\:{Sir}\right) \\ $$$$…………………………………… \\ $$
