Question Number 177768 by Linton last updated on 08/Oct/22

$${use}\:{pertfectly}\:{square}\:{numbers}\:{to}\:{find} \\ $$$$\sqrt{\mathrm{11}} \\ $$$${no}\:{calculators}\:{allowed} \\ $$
Commented by Linton last updated on 09/Oct/22
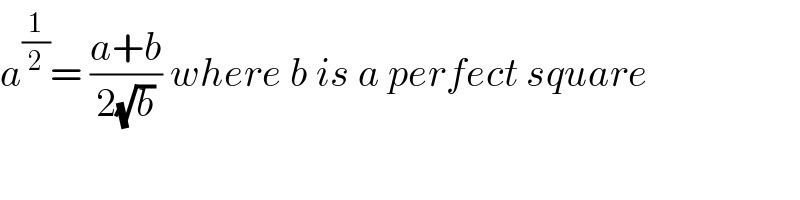
$${a}^{\frac{\mathrm{1}}{\mathrm{2}}} =\:\frac{{a}+{b}}{\mathrm{2}\sqrt{{b}}}\:{where}\:{b}\:{is}\:{a}\:{perfect}\:{square} \\ $$
Answered by a.lgnaoui last updated on 09/Oct/22
![3^2 +((√2) )^2 =(3+(√2) )^2 −6(√2) =(3−2(√2) )^2 −18 =[(3−2(√2) −9]^2 −9^2 =2^2 (3+(√2) )^2 −9^2](https://www.tinkutara.com/question/Q177781.png)
$$\mathrm{3}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} =\left(\mathrm{3}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$=\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} −\mathrm{18} \\ $$$$=\left[\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{9}\right]^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \right. \\ $$$$=\mathrm{2}^{\mathrm{2}} \left(\mathrm{3}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \\ $$
