Question Number 46959 by rahul 19 last updated on 03/Nov/18
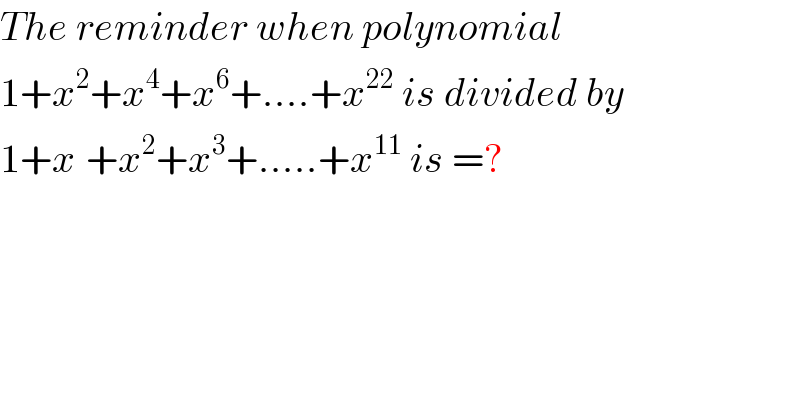
$${The}\:{reminder}\:{when}\:{polynomial} \\ $$$$\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} +….+{x}^{\mathrm{22}} \:{is}\:{divided}\:{by} \\ $$$$\mathrm{1}+{x}^{} +{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…..+{x}^{\mathrm{11}} \:{is}\:=? \\ $$
Commented by rahul 19 last updated on 03/Nov/18

$${I}\:'\:{m}\:{getting}\:\mathrm{2}\:{which}\:{is}\:{wrong}! \\ $$$${we}\:{can}\:{see}\:{they}\:{both}\:{forms}\:{a}\:{G}.{P} \\ $$$$\Rightarrow{remainder}\:{when}\:\:\frac{{x}^{\mathrm{12}} +\mathrm{1}}{{x}+\mathrm{1}}\:=\:\mathrm{2} \\ $$$$\left({cancelling}\:{common}\:{terms}….\right) \\ $$$${Where}\:{am}\:{i}\:{wrong}?? \\ $$
Commented by maxmathsup by imad last updated on 03/Nov/18
![let p(x)=1+x^2 +x^4 +...+x^(22) ⇒p(x)=1+x^2 +(x^2 )^2 +...(x^2 )^(11) = ((1−(x^2 )^(12) )/(1−x^2 )) if x^2 ≠1 ⇒ p(x)=((x^(24) −1)/(x^2 −1)) let q(x)=1+x+x^2 +...x^(11) ⇒ q(x)=((1−x^(12) )/(1−x)) if x≠1 ⇒((p(x)/(q(x))) =((x^(24) −1)/(x^2 −1)) ((x−1)/(x^(12) −1)) = ((x^(24) −1)/((x+1)(x^(12) −1))) =(((x^(12) )^2 −1)/((x+1)(x^(12) −1))) =((x^(12) +1)/(x+1)) x^(12) +1 =0 ⇒x^(12) =e^(i(2k+1)π) ⇒the roots are x_k =e^(i(((2k+1)π)/(12))) k∈[[0,11]] ⇒ x^(12) +1 =Π_(k=0) ^(11) (x−e^(i(((2k+1)π)/(12))) ) ⇒ R(x) =((Π_(k=0) ^(11) (x−e^(i(((2k+1)π)/n)) ))/(x+1))](https://www.tinkutara.com/question/Q46979.png)
$${let}\:{p}\left({x}\right)=\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \:+…+{x}^{\mathrm{22}} \:\Rightarrow{p}\left({x}\right)=\mathrm{1}+{x}^{\mathrm{2}} \:+\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} \:+…\left({x}^{\mathrm{2}} \right)^{\mathrm{11}} \\ $$$$=\:\frac{\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{\mathrm{12}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:{if}\:{x}^{\mathrm{2}} \neq\mathrm{1}\:\Rightarrow\:{p}\left({x}\right)=\frac{{x}^{\mathrm{24}} −\mathrm{1}}{{x}^{\mathrm{2}} \:−\mathrm{1}}\:\:{let}\:{q}\left({x}\right)=\mathrm{1}+{x}+{x}^{\mathrm{2}} \:+…{x}^{\mathrm{11}} \:\Rightarrow \\ $$$${q}\left({x}\right)=\frac{\mathrm{1}−{x}^{\mathrm{12}} }{\mathrm{1}−{x}}\:{if}\:{x}\neq\mathrm{1}\:\Rightarrow\frac{{p}\left({x}\right.}{{q}\left({x}\right)}\:=\frac{{x}^{\mathrm{24}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\frac{{x}−\mathrm{1}}{{x}^{\mathrm{12}} −\mathrm{1}}\:=\:\frac{{x}^{\mathrm{24}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{12}} −\mathrm{1}\right)} \\ $$$$=\frac{\left({x}^{\mathrm{12}} \right)^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{12}} −\mathrm{1}\right)}\:=\frac{{x}^{\mathrm{12}} \:+\mathrm{1}}{{x}+\mathrm{1}} \\ $$$${x}^{\mathrm{12}} +\mathrm{1}\:=\mathrm{0}\:\Rightarrow{x}^{\mathrm{12}} ={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow{the}\:{roots}\:{are}\:{x}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}} \:\:{k}\in\left[\left[\mathrm{0},\mathrm{11}\right]\right]\:\Rightarrow \\ $$$${x}^{\mathrm{12}} \:+\mathrm{1}\:=\prod_{{k}=\mathrm{0}} ^{\mathrm{11}} \:\left({x}−{e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{12}}} \right)\:\Rightarrow\:{R}\left({x}\right)\:=\frac{\prod_{{k}=\mathrm{0}} ^{\mathrm{11}} \left({x}−{e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \right)}{{x}+\mathrm{1}} \\ $$
Commented by MJS last updated on 03/Nov/18

$$\frac{{x}^{\mathrm{12}} +\mathrm{1}}{{x}+\mathrm{1}}={x}^{\mathrm{11}} −{x}^{\mathrm{10}} +{x}^{\mathrm{9}} −{x}^{\mathrm{8}} …+{x}−\mathrm{1}+\frac{\mathrm{2}}{{x}+\mathrm{1}} \\ $$
Commented by maxmathsup by imad last updated on 03/Nov/18

$${thanks}\:{sir}\:{for}\:{this}\:{remak}. \\ $$
Commented by rahul 19 last updated on 04/Nov/18
thanks sir!����
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Nov/18

$${S}_{\mathrm{1}} =\frac{\mathrm{1}\left\{\left({x}^{\mathrm{2}} \right)^{{n}_{\mathrm{1}} } −\mathrm{1}\right\}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${now}\:\mathrm{1}×\left({x}^{\mathrm{2}} \right)^{{n}_{\mathrm{1}} −\mathrm{1}} ={x}^{\mathrm{22}} \:\:\:{n}_{\mathrm{1}} =\mathrm{12} \\ $$$${S}_{\mathrm{2}} =\frac{\mathrm{1}\left\{{x}^{{n}_{\mathrm{2}} } −\mathrm{1}\right\}}{{x}−\mathrm{1}} \\ $$$${x}^{{n}_{\mathrm{2}} −\mathrm{1}} ={x}^{\mathrm{11}} \:\:\:{n}_{\mathrm{2}} =\mathrm{12} \\ $$$$\frac{{S}_{\mathrm{1}} }{{S}_{\mathrm{2}} }=\frac{\frac{\left({x}^{\mathrm{2}} \right)^{\mathrm{12}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}}{\frac{{x}^{\mathrm{12}} −\mathrm{1}}{{x}−\mathrm{1}}}=\frac{\left({x}^{\mathrm{12}} +\mathrm{1}\right)\left({x}^{\mathrm{12}} −\mathrm{1}\right)×{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)×\left({x}^{\mathrm{12}} −\mathrm{1}\right)} \\ $$$$=\frac{{x}^{\mathrm{12}} +\mathrm{1}}{{x}+\mathrm{1}} \\ $$$${R}=\left(−\mathrm{1}\right)^{\mathrm{12}} +\mathrm{1}=\mathrm{2} \\ $$
Commented by rahul 19 last updated on 03/Nov/18

$${Sir},\:{correct}\:{answer}\:{is}\: \\ $$$$\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +…..+{x}^{\mathrm{10}} \right).. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Nov/18

$${is}\:{it}\:{possible}\:…{let}\:{other}\:{solve}\:{the}\:{question}…{i}\: \\ $$$${dl}\:{no}\:{think}\:{so}… \\ $$
Commented by $@ty@m last updated on 03/Nov/18

$${x}+\mathrm{1}\mid{x}^{\mathrm{12}} +\mathrm{1}\mid{x}^{\mathrm{11}} −{x}^{\mathrm{10}} …..−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{12}} +{x}^{\mathrm{11}} \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−{x}^{\mathrm{11}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:−{x}^{\mathrm{11}} −{x}^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{10}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:……… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:……… \\ $$$$\:\:\:\:\:\:\:\:\:−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Commented by rahul 19 last updated on 04/Nov/18
thank you sirs! ����
