Question Number 178323 by mr W last updated on 15/Oct/22
Commented by mr W last updated on 15/Oct/22
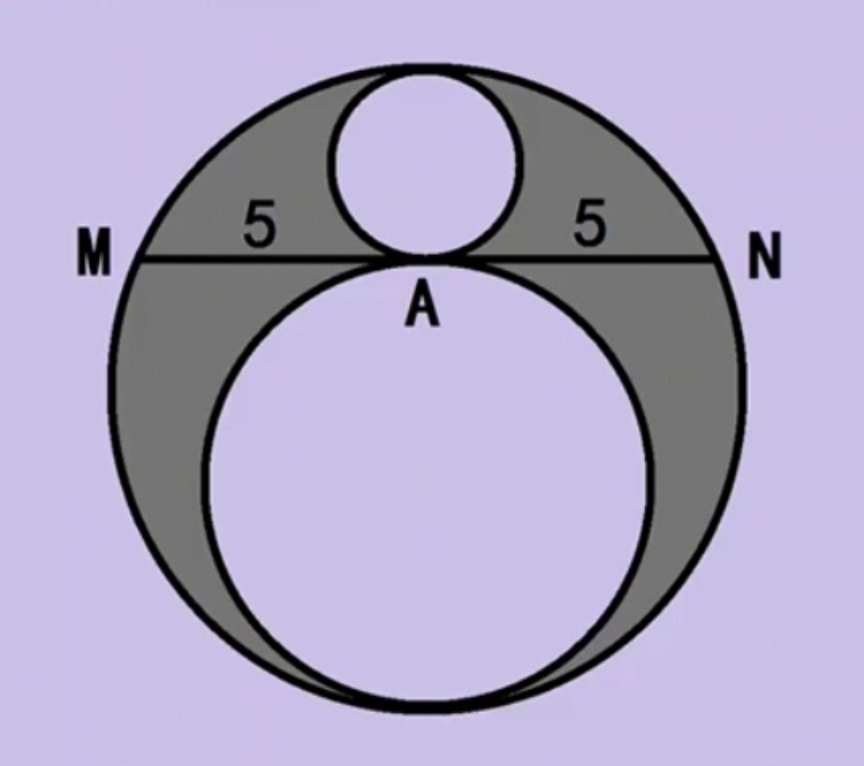
$${find}\:{shaded}\:{area} \\ $$
Commented by cortano1 last updated on 15/Oct/22

$$\frac{\mathrm{25}}{\mathrm{2}}\pi\:\mathrm{unit}\:\mathrm{square}? \\ $$
Commented by mr W last updated on 15/Oct/22

$${yes}\:{sir}! \\ $$
Answered by mr W last updated on 15/Oct/22
Commented by mr W last updated on 15/Oct/22
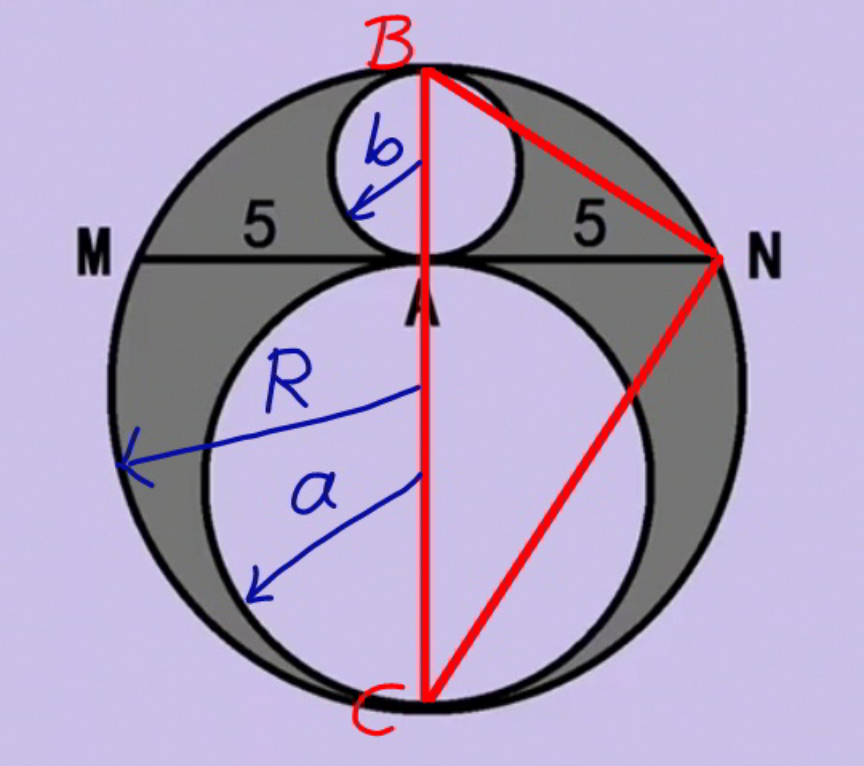
![R=a+b ((AB)/(AN))=((AN)/(AC)) ⇒(2a)(2b)=5^2 ⇒2ab=(5^2 /2) shaded area=πR^2 −πa^2 −πb^2 =π[(a+b)^2 −a^2 −b^2 ] =2abπ =((5^2 π)/2) =12.5π](https://www.tinkutara.com/question/Q178334.png)
$${R}={a}+{b} \\ $$$$\frac{{AB}}{{AN}}=\frac{{AN}}{{AC}} \\ $$$$\Rightarrow\left(\mathrm{2}{a}\right)\left(\mathrm{2}{b}\right)=\mathrm{5}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{ab}=\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${shaded}\:{area}=\pi{R}^{\mathrm{2}} −\pi{a}^{\mathrm{2}} −\pi{b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\pi\left[\left({a}+{b}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{ab}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5}^{\mathrm{2}} \pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{12}.\mathrm{5}\pi \\ $$
Commented by Tawa11 last updated on 15/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
