Question-112882

Question Number 112882 by bemath last updated on 10/Sep/20

Commented by bemath last updated on 10/Sep/20

prof MJs,prof Mr Abdo and other can you help me?

$$\mathrm{prof}\:\mathrm{MJs},\mathrm{prof}\:\mathrm{Mr}\:\mathrm{Abdo}\:\mathrm{and}\:\mathrm{other} \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}? \\ $$

Commented by mathmax by abdo last updated on 10/Sep/20

all i know and all i have in my storeis that 0 is a even number. (at form 2K)

$$\mathrm{all}\:\mathrm{i}\:\mathrm{know}\:\:\mathrm{and}\:\:\mathrm{all}\:\mathrm{i}\:\mathrm{have}\:\mathrm{in}\:\mathrm{my}\:\mathrm{storeis}\:\mathrm{that}\:\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{even}\:\mathrm{number}. \\ $$$$\left(\mathrm{at}\:\mathrm{form}\:\mathrm{2K}\right) \\ $$

Answered by mr W last updated on 10/Sep/20

Commented by bemath last updated on 10/Sep/20

thank you mr W. maybe you have pdf file or book?

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mr}\:\mathrm{W}.\:\mathrm{maybe}\:\mathrm{you}\:\mathrm{have} \\ $$$$\mathrm{pdf}\:\mathrm{file}\:\mathrm{or}\:\mathrm{book}? \\ $$

Commented by bemath last updated on 10/Sep/20

i agree with all sir that zero is an even number, but my colleagues ask if there is any book explaining that. they say zero is also divisible by 3. they say zero is not a number and not an odd number. it is an independent number.

Commented by MJS_new last updated on 10/Sep/20

6 is also divisible by 2 and 3 if 0 is “independent”, what makes it independent, as it behaves exactly like all the even numbers? the sum of 2 even numbers is even 0+24=24 the sum of 2 odd numbers is even −5+5=0 the sum of 1 odd and 1 even number is odd 0+3=3 you would have to say “0 is independent as long it doesn′t interact”.

$$\mathrm{6}\:\mathrm{is}\:\mathrm{also}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3} \\ $$$$\mathrm{if}\:\mathrm{0}\:\mathrm{is}\:“\mathrm{independent}'',\:\mathrm{what}\:\mathrm{makes}\:\mathrm{it}\:\mathrm{independent}, \\ $$$$\mathrm{as}\:\mathrm{it}\:\mathrm{behaves}\:\mathrm{exactly}\:\mathrm{like}\:\mathrm{all}\:\mathrm{the}\:\mathrm{even}\:\mathrm{numbers}? \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{2}\:\mathrm{even}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{0}+\mathrm{24}=\mathrm{24} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{2}\:\mathrm{odd}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{even} \\ $$$$−\mathrm{5}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{1}\:\mathrm{odd}\:\mathrm{and}\:\mathrm{1}\:\mathrm{even}\:\mathrm{number}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\mathrm{0}+\mathrm{3}=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{you}\:\mathrm{would}\:\mathrm{have}\:\mathrm{to}\:\mathrm{say}\:“\mathrm{0}\:\mathrm{is}\:\mathrm{independent}\:\mathrm{as} \\ $$$$\mathrm{long}\:\mathrm{it}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{interact}''. \\ $$

Answered by MJS_new last updated on 10/Sep/20

a number z∈Z is called “even” ⇔ the remainder of its division by 2 is 0 this is a definition. a definition cannot be right or wrong. we can only test a hypothesis: assume 17 is even 17:2=8 remainder 1 but 1≠0 ⇒ 17 is not even assume 0 is even 0:2=0 remainder 0 ⇒ 0 is even

$$\mathrm{a}\:\mathrm{number}\:{z}\in\mathbb{Z}\:\mathrm{is}\:\mathrm{called}\:“\mathrm{even}''\:\Leftrightarrow\:\mathrm{the} \\ $$$$\mathrm{remainder}\:\mathrm{of}\:\mathrm{its}\:\mathrm{division}\:\mathrm{by}\:\mathrm{2}\:\mathrm{is}\:\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\boldsymbol{{definition}}.\:\mathrm{a}\:\mathrm{definition}\:\mathrm{cannot}\:\mathrm{be} \\ $$$$\mathrm{right}\:\mathrm{or}\:\mathrm{wrong}. \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{test}\:\mathrm{a}\:\mathrm{hypothesis}: \\ $$$$ \\ $$$$\mathrm{assume}\:\mathrm{17}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{17}:\mathrm{2}=\mathrm{8}\:\mathrm{remainder}\:\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{1}\neq\mathrm{0}\:\Rightarrow\:\mathrm{17}\:\mathrm{is}\:\mathrm{not}\:\mathrm{even} \\ $$$$ \\ $$$$\mathrm{assume}\:\mathrm{0}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{0}:\mathrm{2}=\mathrm{0}\:\mathrm{remainder}\:\mathrm{0}\:\Rightarrow\:\mathrm{0}\:\mathrm{is}\:\mathrm{even} \\ $$

Commented by bemath last updated on 10/Sep/20

sir. So this a matter that is our debate. : A child will make a password in the form of [letters_1 ],[ number_1 ], [letters_2 ] , [ number_2 ] with condition (1) the first letter is a vowel except I (2) the first number is even (3) the second letter is O (4) the second number are selected from the set { 1,2,4,6,8 }. How many passwords can be generated? my answer is = 4×5×1×5 = 100

$$\mathrm{sir}.\:\mathrm{So}\:\mathrm{this}\:\mathrm{a}\:\mathrm{matter}\:\mathrm{that}\:\mathrm{is}\:\mathrm{our}\:\mathrm{debate}. \\ $$$$:\:\mathrm{A}\:\mathrm{child}\:\mathrm{will}\:\mathrm{make}\:\mathrm{a}\:\mathrm{password}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{form}\:\mathrm{of}\:\left[\mathrm{letters}_{\mathrm{1}} \:\right],\left[\:\mathrm{number}_{\mathrm{1}} \right], \\ $$$$\left[\mathrm{letters}_{\mathrm{2}} \right]\:,\:\left[\:\mathrm{number}_{\mathrm{2}} \right]\:\mathrm{with}\:\mathrm{condition} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{the}\:\mathrm{first}\:\mathrm{letter}\:\mathrm{is}\:\mathrm{a}\:\mathrm{vowel}\:\mathrm{except}\:\mathrm{I} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{the}\:\mathrm{first}\:\mathrm{number}\:\mathrm{is}\:\mathrm{even} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{the}\:\mathrm{second}\:\mathrm{letter}\:\mathrm{is}\:\mathrm{O} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{the}\:\mathrm{second}\:\mathrm{number}\:\mathrm{are}\:\mathrm{selected}\:\mathrm{from}\:\mathrm{the}\: \\ $$$$\mathrm{set}\:\left\{\:\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}\:\right\}. \\ $$$$\mathrm{How}\:\mathrm{many}\:\mathrm{passwords}\:\mathrm{can}\:\mathrm{be}\: \\ $$$$\mathrm{generated}? \\ $$$$\mathrm{my}\:\mathrm{answer}\:\mathrm{is}\:=\:\mathrm{4}×\mathrm{5}×\mathrm{1}×\mathrm{5}\:=\:\mathrm{100} \\ $$

Commented by bemath last updated on 10/Sep/20

$$\mathrm{but}\:\mathrm{my}\:\mathrm{friend}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{80} \\ $$

Commented by MJS_new last updated on 10/Sep/20

your answer is right because 0 is even. try to prove it is not even... if somebody has a proof, let me know, I′ll review it

$$\mathrm{your}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{right}\:\mathrm{because}\:\mathrm{0}\:\mathrm{is}\:\mathrm{even}. \\ $$$$\mathrm{try}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{even}…\:\mathrm{if}\:\mathrm{somebody}\:\mathrm{has} \\ $$$$\mathrm{a}\:\mathrm{proof},\:\mathrm{let}\:\mathrm{me}\:\mathrm{know},\:\mathrm{I}'\mathrm{ll}\:\mathrm{review}\:\mathrm{it} \\ $$

Commented by bemath last updated on 10/Sep/20

that's how my colleagues insist that zero is not an even number. my emotions were bought. they argue which book explains that it is an even number

Answered by $@y@m last updated on 10/Sep/20

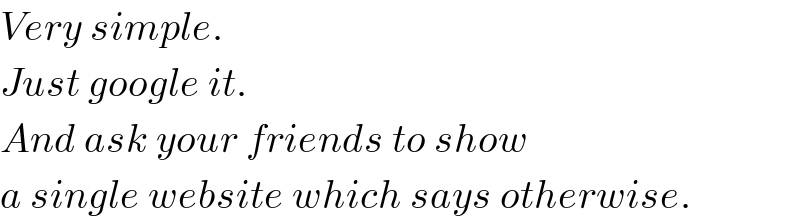
$${Very}\:{simple}. \\ $$$${Just}\:{google}\:{it}. \\ $$$${And}\:{ask}\:{your}\:{friends}\:{to}\:{show} \\ $$$${a}\:{single}\:{website}\:{which}\:{says}\:{otherwise}. \\ $$

Commented by mathmax by abdo last updated on 11/Sep/20

its seems that you are open a door of philosofy....

$$\mathrm{its}\:\mathrm{seems}\:\mathrm{that}\:\mathrm{you}\:\mathrm{are}\:\mathrm{open}\:\mathrm{a}\:\mathrm{door}\:\mathrm{of}\:\mathrm{philosofy}…. \\ $$

Commented by $@y@m last updated on 11/Sep/20

�� The question itself is philosophy. Mr. Bemath knows 0 is an even number. The problem is how to convince his friend.

Commented by MJS_new last updated on 11/Sep/20

The problem is, you cannot convince anybody who doesn′t want to follow your arguments. I remember a person here who “proved” that i=(√(−1))=±1, other people believe π is wrong because its “true” value is 6.283185... not 3.141592... I also remember some fights with someone who believes 5−2×3=9.

$$\mathrm{The}\:\mathrm{problem}\:\mathrm{is},\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{convince}\:\mathrm{anybody} \\ $$$$\mathrm{who}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{want}\:\mathrm{to}\:\mathrm{follow}\:\mathrm{your}\:\mathrm{arguments}. \\ $$$$\mathrm{I}\:\mathrm{remember}\:\mathrm{a}\:\mathrm{person}\:\mathrm{here}\:\mathrm{who}\:“\mathrm{proved}''\:\mathrm{that} \\ $$$$\mathrm{i}=\sqrt{−\mathrm{1}}=\pm\mathrm{1},\:\mathrm{other}\:\mathrm{people}\:\mathrm{believe}\:\pi\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{because}\:\mathrm{its}\:“\mathrm{true}''\:\mathrm{value}\:\mathrm{is}\:\mathrm{6}.\mathrm{283185}…\:\mathrm{not} \\ $$$$\mathrm{3}.\mathrm{141592}…\:\mathrm{I}\:\mathrm{also}\:\mathrm{remember}\:\mathrm{some}\:\mathrm{fights}\:\mathrm{with} \\ $$$$\mathrm{someone}\:\mathrm{who}\:\mathrm{believes}\:\mathrm{5}−\mathrm{2}×\mathrm{3}=\mathrm{9}. \\ $$

Commented by MJS_new last updated on 11/Sep/20

definition: ∀n∈Z: if the division n:2 leaves the reminder 0 we call n even this is all we need. n can be { ((even)),((not even = uneven =odd)),((undecideable)) :} examples: even: −16; 542; 6u+2∀u∈Z; 2p^2 −18∀p∈Z generally 2k∀k∈Z odd: −371; 3; 8h−1∀h∈Z; 2s^2 −4t^4 +1∀s, t ∈Z generally 2k+1∀k∈Z undecideable: e∈Z; u×v∧u, v ∈Z, h^3 +5∧h∈Z thesis: 0 is odd prove: 0∈Z ⇒ 0 is odd ⇔ ∃k∈Z: 2k+1=0 2k+1=0 ∣−1 2k=−1 ∣÷2 k=−(1/2) ∉Z ⇒ false ⇒ 0 is not odd thesis: 0 is even prove: 0∈Z ⇒ 0 is even ⇔ ∃k∈Z:2k=0 2k=0 ∣÷2 k=0 testing: 2k=2×0=0 ⇒ 0 is even note: if n∉Z we might need additional definitions ((p/q) divided by 2 = (p/(2q)) remainder 0 ⇒^(???) (p/q)∈Q even)

$$\boldsymbol{\mathrm{definition}}:\:\forall\boldsymbol{{n}}\in\mathbb{Z}:\:\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{division}}\:\boldsymbol{{n}}:\mathrm{2}\:\boldsymbol{\mathrm{leaves}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{reminder}}\:\mathrm{0}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{call}}\:\boldsymbol{{n}}\:\boldsymbol{\mathrm{even}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{all}\:\mathrm{we}\:\mathrm{need}. \\ $$$${n}\:\mathrm{can}\:\mathrm{be}\:\begin{cases}{\mathrm{even}}\\{\mathrm{not}\:\mathrm{even}\:=\:\mathrm{uneven}\:=\mathrm{odd}}\\{\mathrm{undecideable}}\end{cases} \\ $$$$\mathrm{examples}: \\ $$$$\mathrm{even}:\:−\mathrm{16};\:\mathrm{542};\:\mathrm{6}{u}+\mathrm{2}\forall{u}\in\mathbb{Z};\:\mathrm{2}{p}^{\mathrm{2}} −\mathrm{18}\forall{p}\in\mathbb{Z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{generally}\:\mathrm{2}{k}\forall{k}\in\mathbb{Z} \\ $$$$\mathrm{odd}:\:\:\:−\mathrm{371};\:\mathrm{3};\:\mathrm{8}{h}−\mathrm{1}\forall{h}\in\mathbb{Z};\:\mathrm{2}{s}^{\mathrm{2}} −\mathrm{4}{t}^{\mathrm{4}} +\mathrm{1}\forall{s},\:{t}\:\in\mathbb{Z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{generally}\:\mathrm{2}{k}+\mathrm{1}\forall{k}\in\mathbb{Z} \\ $$$$\mathrm{undecideable}:\:{e}\in\mathbb{Z};\:{u}×{v}\wedge{u},\:{v}\:\in\mathbb{Z},\:{h}^{\mathrm{3}} +\mathrm{5}\wedge{h}\in\mathbb{Z} \\ $$$$ \\ $$$$\mathrm{thesis}:\:\mathrm{0}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\mathrm{prove}:\:\mathrm{0}\in\mathbb{Z}\:\Rightarrow\:\mathrm{0}\:\mathrm{is}\:\mathrm{odd}\:\Leftrightarrow\:\exists{k}\in\mathbb{Z}:\:\mathrm{2}{k}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{k}+\mathrm{1}=\mathrm{0}\:\:\:\:\:\mid−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{k}=−\mathrm{1}\:\:\:\:\:\:\:\mid\boldsymbol{\div}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}=−\frac{\mathrm{1}}{\mathrm{2}}\:\notin\mathbb{Z}\:\Rightarrow\:\mathrm{false}\:\Rightarrow\:\mathrm{0}\:\mathrm{is}\:\mathrm{not}\:\mathrm{odd} \\ $$$$\mathrm{thesis}:\:\mathrm{0}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{prove}:\:\mathrm{0}\in\mathbb{Z}\:\Rightarrow\:\mathrm{0}\:\mathrm{is}\:\mathrm{even}\:\Leftrightarrow\:\exists{k}\in\mathbb{Z}:\mathrm{2}{k}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{k}=\mathrm{0}\:\:\:\:\:\:\mid\boldsymbol{\div}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{testing}:\:\mathrm{2}{k}=\mathrm{2}×\mathrm{0}=\mathrm{0}\:\Rightarrow\:\mathrm{0}\:\mathrm{is}\:\mathrm{even} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{note}}:\:\boldsymbol{\mathrm{if}}\:\boldsymbol{{n}}\notin\mathbb{Z}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{might}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{additional}}\:\boldsymbol{\mathrm{definitions}} \\ $$$$\left(\frac{{p}}{{q}}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{2}\:=\:\frac{{p}}{\mathrm{2}{q}}\:\mathrm{remainder}\:\mathrm{0}\:\overset{???} {\Rightarrow}\:\frac{{p}}{{q}}\in\mathbb{Q}\:\mathrm{even}\right) \\ $$

Commented by bemath last updated on 11/Sep/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{prof} \\ $$

Commented by abdomsup last updated on 11/Sep/20

simple he must give them a pizza if they are two he divide the pizza by 2 and him dont eat of they are tre he divide the pizza by 4 and eat with them....

$${simple}\:{he}\:{must}\:{give}\:{them}\:{a}\:{pizza} \\ $$$${if}\:\:{they}\:{are}\:{two}\:{he}\:{divide}\:{the}\: \\ $$$${pizza}\:{by}\:\mathrm{2}\:\:{and}\:{him}\:{dont}\:{eat} \\ $$$${of}\:{they}\:{are}\:{tre}\:\:{he}\:{divide}\:{the} \\ $$$${pizza}\:{by}\:\mathrm{4}\:{and}\:{eat}\:{with}\:{them}…. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply