Question Number 47471 by ajfour last updated on 10/Nov/18
Commented by ajfour last updated on 10/Nov/18

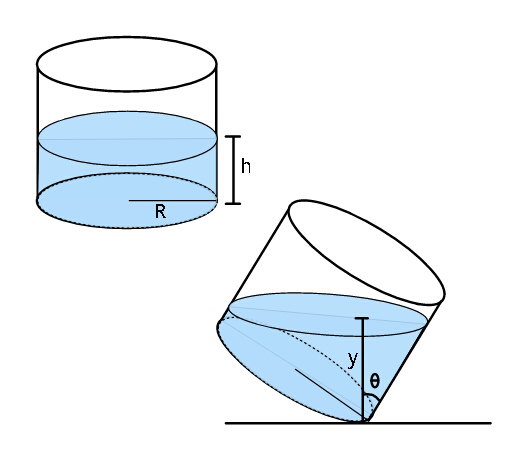
$${Find}\:\:{y}\left(\theta\right). \\ $$
Commented by peter frank last updated on 25/Dec/21

$$\mathrm{what}\:\mathrm{is}\:\mathrm{name}\:\mathrm{of}\:\mathrm{this}\:\mathrm{app} \\ $$
Answered by MrW3 last updated on 11/Nov/18
![volume of water V=πR^2 h θ_m =tan^(−1) (h/R) case 1: θ≤θ_m bottom of cantainer is submerged. πR^2 (h_1 +h_2 )/2=πR^2 h ⇒h_1 +h_2 =2h h_2 −h_1 =2R tan θ ⇒h_2 =h+R tan θ y=h_2 cos θ=(h+R tan θ) cos θ ⇒y(θ)=R sin θ+h cos θ with θ≤θ_m case 2: θ>θ_m bottom of container is not completely submerged. h_3 =R(1−cos α) h_2 =h_3 tan θ=R(1−cos α)tan θ A=(R^2 /2)(2α−sin 2α)=R^2 (α−sin α cos α) V=((Ah_2 )/2)=((R^3 (α−sin α cos α)(1−cos α)tan θ)/2)=πR^2 h ⇒((R(α−sin α cos α)(1−cos α)tan θ)/2)=πh ⇒(α−sin α cos α)(1−cos α)=((2πh)/(R tan θ)) ⇒α=α(θ) (only numerically) y=h_2 cos θ ⇒y(θ)=R[1−cos α(θ)]sin θ](https://www.tinkutara.com/question/Q47496.png)
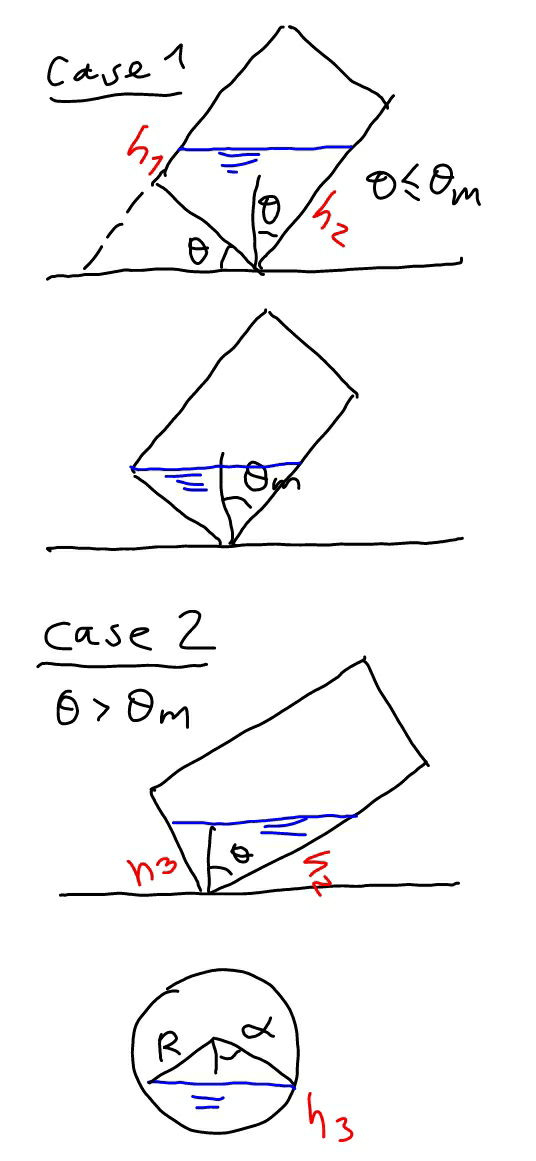
$${volume}\:{of}\:{water}\:{V}=\pi{R}^{\mathrm{2}} {h} \\ $$$$\theta_{{m}} =\mathrm{tan}^{−\mathrm{1}} \frac{{h}}{{R}} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:\theta\leqslant\theta_{{m}} \\ $$$${bottom}\:{of}\:{cantainer}\:{is}\:{submerged}. \\ $$$$\pi{R}^{\mathrm{2}} \left({h}_{\mathrm{1}} +{h}_{\mathrm{2}} \right)/\mathrm{2}=\pi{R}^{\mathrm{2}} {h} \\ $$$$\Rightarrow{h}_{\mathrm{1}} +{h}_{\mathrm{2}} =\mathrm{2}{h} \\ $$$${h}_{\mathrm{2}} −{h}_{\mathrm{1}} =\mathrm{2}{R}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{h}_{\mathrm{2}} ={h}+{R}\:\mathrm{tan}\:\theta \\ $$$${y}={h}_{\mathrm{2}} \mathrm{cos}\:\theta=\left({h}+{R}\:\mathrm{tan}\:\theta\right)\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{y}\left(\theta\right)={R}\:\mathrm{sin}\:\theta+{h}\:\mathrm{cos}\:\theta\:{with}\:\theta\leqslant\theta_{{m}} \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:\theta>\theta_{{m}} \\ $$$${bottom}\:{of}\:{container}\:{is}\:{not}\:{completely} \\ $$$${submerged}. \\ $$$${h}_{\mathrm{3}} ={R}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right) \\ $$$${h}_{\mathrm{2}} ={h}_{\mathrm{3}} \:\mathrm{tan}\:\theta={R}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)\mathrm{tan}\:\theta \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha\right)={R}^{\mathrm{2}} \left(\alpha−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\right) \\ $$$${V}=\frac{{Ah}_{\mathrm{2}} }{\mathrm{2}}=\frac{{R}^{\mathrm{3}} \left(\alpha−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)\mathrm{tan}\:\theta}{\mathrm{2}}=\pi{R}^{\mathrm{2}} {h} \\ $$$$\Rightarrow\frac{{R}\left(\alpha−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)\mathrm{tan}\:\theta}{\mathrm{2}}=\pi{h} \\ $$$$\Rightarrow\left(\alpha−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)=\frac{\mathrm{2}\pi{h}}{{R}\:\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\alpha=\alpha\left(\theta\right)\:\left({only}\:{numerically}\right) \\ $$$${y}={h}_{\mathrm{2}} \:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{y}\left(\theta\right)={R}\left[\mathrm{1}−\mathrm{cos}\:\alpha\left(\theta\right)\right]\mathrm{sin}\:\theta \\ $$
Commented by MrW3 last updated on 10/Nov/18