Question Number 113738 by bemath last updated on 15/Sep/20
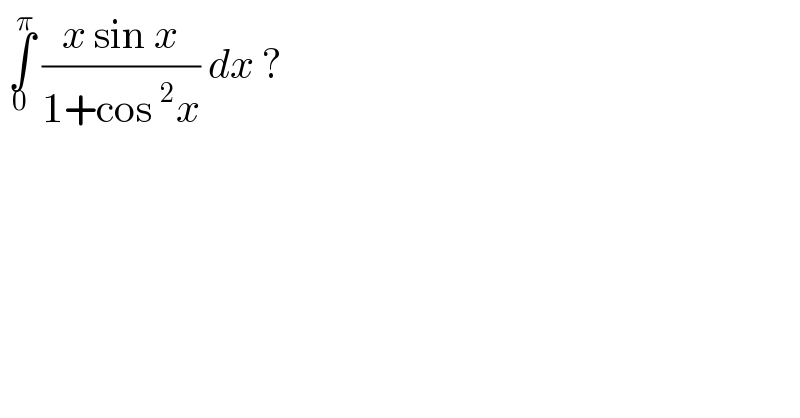
$$\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{x}\:\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:? \\ $$
Answered by bobhans last updated on 15/Sep/20
![I = ∫_0 ^π ((x sin x)/(1+cos^2 x)) dx replace x by π−x →I=∫_π ^0 (((π−x)sin (π−x))/(1+cos^2 (π−x))) (−dx) I= ∫_0 ^π (((π−x)sin x)/(1+cos^2 x)) dx = ∫_0 ^π ((πsin x)/(1+cos^2 x)) dx−∫_0 ^π ((xsin x)/(1+cos^2 x)) dx 2I = ∫_0 ^π ((π sin x)/(1+cos^2 x)) dx consider ∫ ((π sin x)/(1+cos x))dx = −π∫ ((d(cos x))/(1+cos^2 x)) = −π∫ (du/(1+u^2 )) = −π tan^(−1) (cos x) + c now we have 2I = −π [ tan^(−1) (cos x) ]_0 ^π I = −(π/2)[−(π/4)−(π/4) ]= (π^2 /4).](https://www.tinkutara.com/question/Q113739.png)
$$\mathrm{I}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{replace}\:\mathrm{x}\:\mathrm{by}\:\pi−\mathrm{x}\:\rightarrow\mathrm{I}=\underset{\pi} {\overset{\mathrm{0}} {\int}}\:\frac{\left(\pi−\mathrm{x}\right)\mathrm{sin}\:\left(\pi−\mathrm{x}\right)}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)}\:\left(−\mathrm{dx}\right) \\ $$$$\mathrm{I}=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\left(\pi−\mathrm{x}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\pi\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}−\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{xsin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{2I}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\pi\:\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{consider}\:\int\:\frac{\pi\:\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\mathrm{dx}\:=\:−\pi\int\:\frac{\mathrm{d}\left(\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\pi\int\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\pi\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{cos}\:\mathrm{x}\right)\:+\:\mathrm{c}\:\:\:\:\:\: \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{2I}\:=\:−\pi\:\left[\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{cos}\:\mathrm{x}\right)\:\right]_{\mathrm{0}} ^{\pi} \\ $$$$\mathrm{I}\:=\:−\frac{\pi}{\mathrm{2}}\left[−\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{4}}\:\right]=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}. \\ $$$$ \\ $$
