Question Number 49389 by behi83417@gmail.com last updated on 06/Dec/18
![for x≠0,y≠0,xy≠−1,f(1)=(1/2) f(x)+f(y)=f(x+y)+((x+y)/(1+xy)) 1.find: f(x),[if possible] 2.find :f^(−1) (1),[if possible].](https://www.tinkutara.com/question/Q49389.png)
$${for}\:{x}\neq\mathrm{0},{y}\neq\mathrm{0},\mathrm{xy}\neq−\mathrm{1},{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{y}}\right)=\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)+\frac{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}{\mathrm{1}+\boldsymbol{\mathrm{xy}}} \\ $$$$\mathrm{1}.{find}:\:{f}\left({x}\right),\left[{if}\:{possible}\right] \\ $$$$\mathrm{2}.{find}\::{f}^{−\mathrm{1}} \left(\mathrm{1}\right),\left[{if}\:{possible}\right]. \\ $$
Answered by kaivan.ahmadi last updated on 07/Dec/18
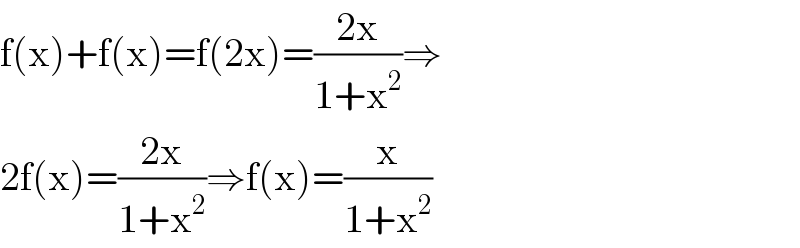
$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{2x}\right)=\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\Rightarrow \\ $$$$\mathrm{2f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$
Commented by Abdo msup. last updated on 08/Dec/18
![f(x)=y ⇔x=f^(−1) (y) f(x)=y ⇔(x/(1+x^2 )) =y ⇔x=(1+x^2 )y ⇔y +yx^2 −x =0 ⇔yx^2 −x +y =0 Δ=1−4y^2 Δ≥0 ⇔ 4y^2 ≤1 ⇔∣y∣≤(1/2) x_1 =((1+(√(1−4y^2 )))/(2y)) and x_2 =((1−(√(1−4y^2 )))/(2y)) ⇒ f^(−1) (y) =((1 +^− (√(1−4y^2 )))/(2y)) and we see that f^(−1) (1)dont exist ( 1∉[−(1/2) ,(1/2)])](https://www.tinkutara.com/question/Q49580.png)
$${f}\left({x}\right)={y}\:\Leftrightarrow{x}={f}^{−\mathrm{1}} \left({y}\right)\: \\ $$$${f}\left({x}\right)={y}\:\Leftrightarrow\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={y}\:\Leftrightarrow{x}=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}\:\Leftrightarrow{y}\:+{yx}^{\mathrm{2}} −{x}\:=\mathrm{0} \\ $$$$\Leftrightarrow{yx}^{\mathrm{2}} −{x}\:+{y}\:=\mathrm{0} \\ $$$$\Delta=\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} \:\:\:\:\Delta\geqslant\mathrm{0}\:\Leftrightarrow\:\mathrm{4}{y}^{\mathrm{2}} \leqslant\mathrm{1}\:\Leftrightarrow\mid{y}\mid\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} }}{\mathrm{2}{y}}\:\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} }}{\mathrm{2}{y}}\:\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({y}\right)\:=\frac{\mathrm{1}\:\overset{−} {+}\sqrt{\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} }}{\mathrm{2}{y}}\:\:\:\:{and}\:{we}\:{see}\:{that}\:{f}^{−\mathrm{1}} \left(\mathrm{1}\right){dont}\:{exist} \\ $$$$\left(\:\mathrm{1}\notin\left[−\frac{\mathrm{1}}{\mathrm{2}}\:,\frac{\mathrm{1}}{\mathrm{2}}\right]\right) \\ $$
Answered by kaivan.ahmadi last updated on 07/Dec/18
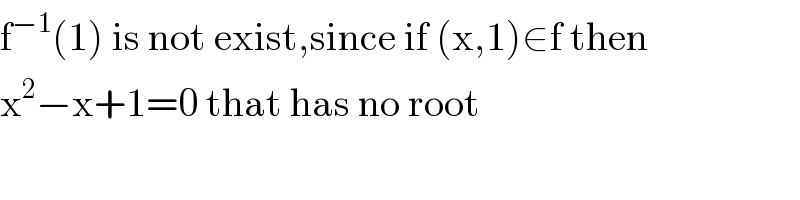
$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{exist},\mathrm{since}\:\mathrm{if}\:\left(\mathrm{x},\mathrm{1}\right)\in\mathrm{f}\:\mathrm{then} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\:\mathrm{that}\:\mathrm{has}\:\mathrm{no}\:\mathrm{root} \\ $$
