Question Number 115489 by ruwedkabeh last updated on 26/Sep/20
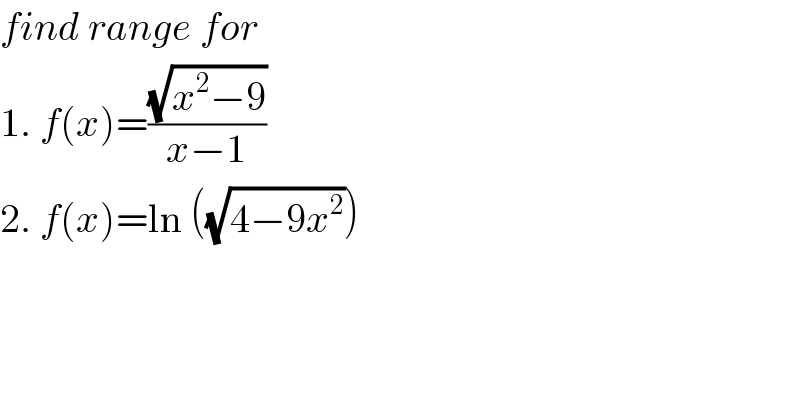
$${find}\:{range}\:{for} \\ $$$$\mathrm{1}.\:{f}\left({x}\right)=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{{x}−\mathrm{1}} \\ $$$$\mathrm{2}.\:{f}\left({x}\right)=\mathrm{ln}\:\left(\sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }\right) \\ $$
Answered by PRITHWISH SEN 2 last updated on 26/Sep/20
![1. Let y= ((√(x^2 −9))/(x−1)) x^2 (y^2 −1)−2xy^2 +(y^2 +9)=0 for real x △ = (2y^2 )^2 −4(y^2 −1)(y^2 +9)≥0 ⇒ (y−(3/(2(√2))))(y+(3/(2(√2))))≤0 Range f(x)∈ [−(3/(2(√2))) , (3/(2(√2))) ] 2. Again let y = ln ((√(4−9x^2 ))) ⇒ e^(2y ) = 4−9x^2 x = ±(1/3)(√(4−e^(2y) )) for x to be real y ≤ ln 2 Range of f(x)∈ (−∞, ln 2]](https://www.tinkutara.com/question/Q115495.png)
$$\mathrm{1}.\:\:\mathrm{Let}\:\mathrm{y}=\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{x}−\mathrm{1}} \\ $$$$\mathrm{x}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2xy}^{\mathrm{2}} +\left(\mathrm{y}^{\mathrm{2}} +\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{for}\:\mathrm{real}\:\mathrm{x} \\ $$$$\bigtriangleup\:=\:\left(\mathrm{2y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{9}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{y}−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\left(\mathrm{y}+\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\leqslant\mathrm{0} \\ $$$$\boldsymbol{\mathrm{Range}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\in\:\left[−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}}\:,\:\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\right] \\ $$$$\mathrm{2}.\:\:\mathrm{Again}\:\mathrm{let}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\:=\:\mathrm{ln}\:\left(\sqrt{\mathrm{4}−\mathrm{9x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\mathrm{e}^{\mathrm{2y}\:} =\:\mathrm{4}−\mathrm{9x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\pm\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{4}−\mathrm{e}^{\mathrm{2y}} }\:\: \\ $$$$\:\:\:\:\mathrm{for}\:\mathrm{x}\:\mathrm{to}\:\mathrm{be}\:\mathrm{real} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{y}\:\leqslant\:\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:\boldsymbol{\mathrm{Range}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\in\:\left(−\infty,\:\mathrm{ln}\:\mathrm{2}\right] \\ $$
Commented by ruwedkabeh last updated on 26/Sep/20
$${Thank}\:{you}\:{very}\:{much}! \\ $$
