Question Number 50328 by peter frank last updated on 15/Dec/18

Answered by peter frank last updated on 16/Dec/18

$$\left.\mathrm{1}\right) \\ $$$${x}+\mathrm{2}{y}−\mathrm{3}{z}={a}…\left({i}\right) \\ $$$$\mathrm{2}{x}+\mathrm{6}{y}−\mathrm{11}{z}={b}…\left({ii}\right) \\ $$$${x}−\mathrm{2}{y}+\mathrm{7}{z}={c}….\left({iii}\right) \\ $$$${eliminate}\:{x} \\ $$$${x}+\mathrm{2}{y}−\mathrm{3}{z}={a}…\left({i}\right) \\ $$$$\mathrm{2}{x}+\mathrm{6}{y}−\mathrm{11}{z}={b}…\left({ii}\right) \\ $$$$−\mathrm{2}{y}+\mathrm{5}{z}=\mathrm{2}{a}−{b}….\left({iv}\right) \\ $$$${eliminate}\:{x} \\ $$$${x}+\mathrm{2}{y}−\mathrm{3}{z}={a}…\left({i}\right) \\ $$$${x}−\mathrm{2}{y}+\mathrm{7}{z}={c}….\left({iii}\right) \\ $$$$\mathrm{4}{y}−\mathrm{10}{z}={a}−{c}….\left({v}\right) \\ $$$${eliminate}\:{y}\:{and}\:{z} \\ $$$$−\mathrm{2}{y}+\mathrm{5}{z}=\mathrm{2}{a}−{b}….\left({iv}\right) \\ $$$$\mathrm{4}{y}−\mathrm{10}{z}={a}−{c}….\left({v}\right) \\ $$$$\mathrm{5}{a}−\mathrm{2b}−{c}=\mathrm{0} \\ $$$$ \\ $$
Answered by peter frank last updated on 16/Dec/18
![2) x+y−z= 1....(i) 2x+3y−ay=3....(ii) x+ay+3z=2....(iii) eliminate x x+y−z= 1....(i) 2x+3y−ay=3....(ii) y+(a+2)z=1....(iv) eliminate x x+y−z= 1....(i) x+ay+3z=2....(iii) y(a−1)+4z=1....(v) eliminate y y+(a+2)z=1....(iv) y(a−1)+4z=1....(v) (a+2)(a−1)−4]z=a−2 (a^2 +a−6)z=a−2 ......](https://www.tinkutara.com/question/Q50437.png)
$$\left.\mathrm{2}\right) \\ $$$${x}+{y}−{z}=\:\mathrm{1}….\left({i}\right) \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}−{ay}=\mathrm{3}….\left({ii}\right) \\ $$$${x}+{ay}+\mathrm{3}{z}=\mathrm{2}….\left({iii}\right) \\ $$$${eliminate}\:{x} \\ $$$${x}+{y}−{z}=\:\mathrm{1}….\left({i}\right) \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}−{ay}=\mathrm{3}….\left({ii}\right) \\ $$$${y}+\left({a}+\mathrm{2}\right){z}=\mathrm{1}….\left({iv}\right) \\ $$$${eliminate}\:{x} \\ $$$${x}+{y}−{z}=\:\mathrm{1}….\left({i}\right) \\ $$$${x}+{ay}+\mathrm{3}{z}=\mathrm{2}….\left({iii}\right) \\ $$$${y}\left({a}−\mathrm{1}\right)+\mathrm{4}{z}=\mathrm{1}….\left({v}\right) \\ $$$${eliminate}\:{y} \\ $$$${y}+\left({a}+\mathrm{2}\right){z}=\mathrm{1}….\left({iv}\right) \\ $$$${y}\left({a}−\mathrm{1}\right)+\mathrm{4}{z}=\mathrm{1}….\left({v}\right) \\ $$$$\left.\left({a}+\mathrm{2}\right)\left({a}−\mathrm{1}\right)−\mathrm{4}\right]{z}={a}−\mathrm{2} \\ $$$$\left({a}^{\mathrm{2}} +{a}−\mathrm{6}\right){z}={a}−\mathrm{2} \\ $$$$ \\ $$$$…… \\ $$
Commented by peter frank last updated on 16/Dec/18
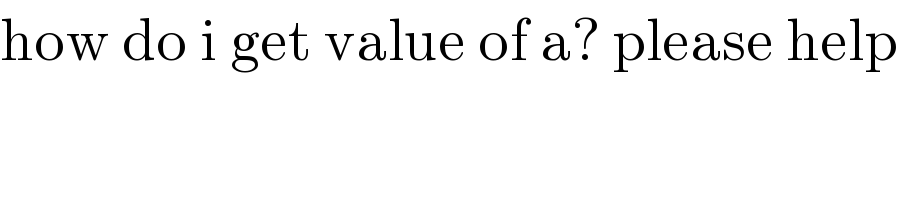
$$\mathrm{how}\:\mathrm{do}\:\mathrm{i}\:\mathrm{get}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}?\:\mathrm{please}\:\mathrm{help} \\ $$
