Question Number 50561 by ajfour last updated on 17/Dec/18
Commented by ajfour last updated on 17/Dec/18
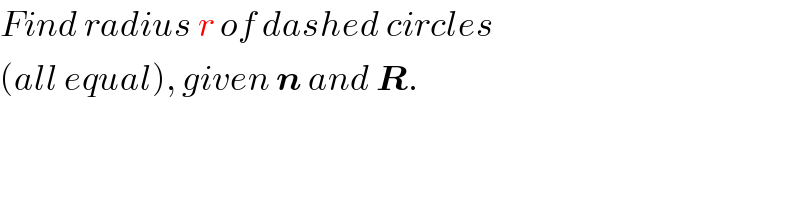
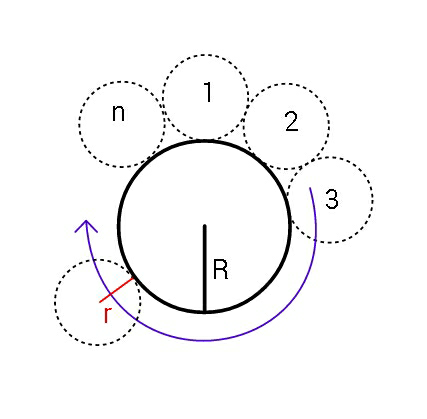
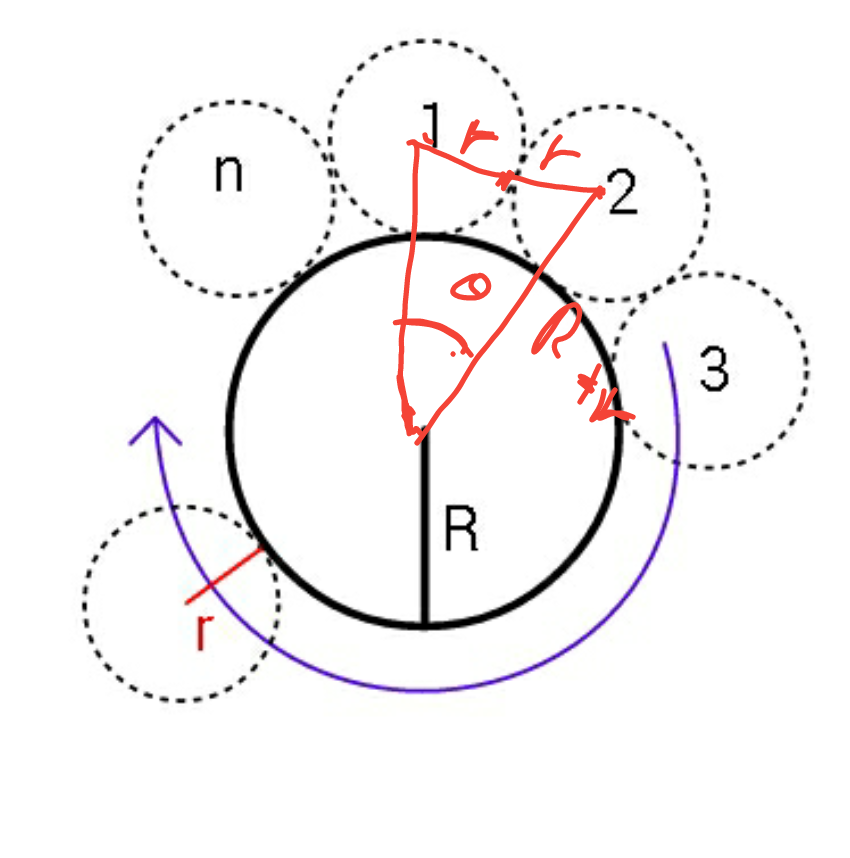
$${Find}\:{radius}\:{r}\:{of}\:{dashed}\:{circles} \\ $$$$\left({all}\:{equal}\right),\:{given}\:\boldsymbol{{n}}\:{and}\:\boldsymbol{{R}}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Dec/18
![joining the centres of n circles make a[circle of radius =R+r join each centre of circle of radius r with centre of circle of radius R (n)θ=2π θ=((2π)/n) cosθ=(((R+r)^2 +(R+r)^2 −(2r)^2 )/(2(R+r)(R+r))) (2r)^2 =2(R+r)^2 −2(R+r)^2 cosθ (2r)^2 =2(R+r)^2 [1−cosθ] (2r)^2 =4(R+r)^2 sin^2 ((θ/2)) 2r=2(R+r)sin((θ/2)) r=(R+r)sin((θ/2)) r−rsin((θ/2))=Rsin((θ/2)) r=((Rsin((θ/2)))/(1−sin((θ/2))))=((Rsin((π/n)))/(1−sin((π/n)))) pls check..](https://www.tinkutara.com/question/Q50571.png)
$${joining}\:{the}\:{centres}\:{of}\:{n}\:{circles}\:{make}\:{a}\left[{circle}\right. \\ $$$${of}\:{radius}\:={R}+{r} \\ $$$${join}\:{each}\:{centre}\:{of}\:\:{circle}\:{of}\:{radius}\:{r}\:{with} \\ $$$${centre}\:{of}\:{circle}\:{of}\:{radius}\:{R} \\ $$$$\left({n}\right)\theta=\mathrm{2}\pi \\ $$$$\theta=\frac{\mathrm{2}\pi}{{n}} \\ $$$${cos}\theta=\frac{\left({R}+{r}\right)^{\mathrm{2}} +\left({R}+{r}\right)^{\mathrm{2}} −\left(\mathrm{2}{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}+{r}\right)\left({R}+{r}\right)} \\ $$$$\left(\mathrm{2}{r}\right)^{\mathrm{2}} =\mathrm{2}\left({R}+{r}\right)^{\mathrm{2}} −\mathrm{2}\left({R}+{r}\right)^{\mathrm{2}} {cos}\theta \\ $$$$\left(\mathrm{2}{r}\right)^{\mathrm{2}} =\mathrm{2}\left({R}+{r}\right)^{\mathrm{2}} \left[\mathrm{1}−{cos}\theta\right] \\ $$$$\left(\mathrm{2}{r}\right)^{\mathrm{2}} =\mathrm{4}\left({R}+{r}\right)^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{r}=\mathrm{2}\left({R}+{r}\right){sin}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$ \\ $$$${r}=\left({R}+{r}\right){sin}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$${r}−{rsin}\left(\frac{\theta}{\mathrm{2}}\right)={Rsin}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$${r}=\frac{{Rsin}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−{sin}\left(\frac{\theta}{\mathrm{2}}\right)}=\frac{{Rsin}\left(\frac{\pi}{{n}}\right)}{\mathrm{1}−{sin}\left(\frac{\pi}{{n}}\right)} \\ $$$${pls}\:{check}.. \\ $$
Commented by ajfour last updated on 18/Dec/18
$${Thanks}\:{Tanmay}\:{Sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Dec/18
$${thank}\:{you}\:{sir}…{ldt}\:{me}\:{rectify}.. \\ $$
Answered by mr W last updated on 17/Dec/18
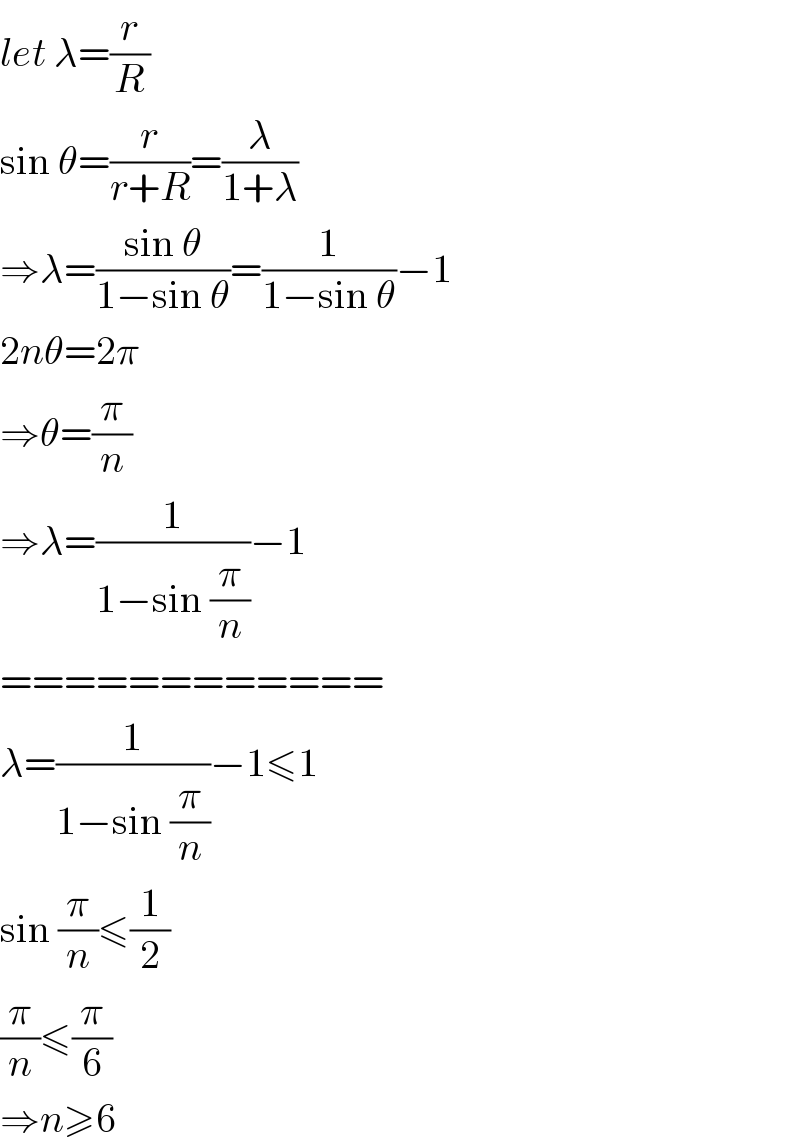
$${let}\:\lambda=\frac{{r}}{{R}} \\ $$$$\mathrm{sin}\:\theta=\frac{{r}}{{r}+{R}}=\frac{\lambda}{\mathrm{1}+\lambda} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{sin}\:\theta}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\theta}−\mathrm{1} \\ $$$$\mathrm{2}{n}\theta=\mathrm{2}\pi \\ $$$$\Rightarrow\theta=\frac{\pi}{{n}} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{{n}}}−\mathrm{1} \\ $$$$============ \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{{n}}}−\mathrm{1}\leqslant\mathrm{1} \\ $$$$\mathrm{sin}\:\frac{\pi}{{n}}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\pi}{{n}}\leqslant\frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow{n}\geqslant\mathrm{6} \\ $$
Commented by mr W last updated on 17/Dec/18
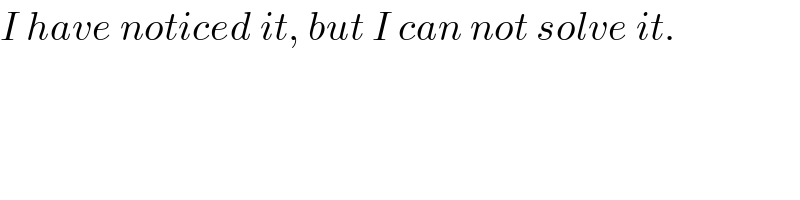
$${I}\:{have}\:{noticed}\:{it},\:{but}\:{I}\:{can}\:{not}\:{solve}\:{it}. \\ $$
Commented by ajfour last updated on 17/Dec/18
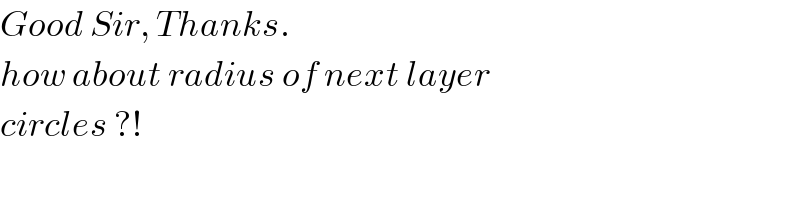
$${Good}\:{Sir},\:{Thanks}. \\ $$$${how}\:{about}\:{radius}\:{of}\:{next}\:{layer} \\ $$$${circles}\:?! \\ $$
Commented by mr W last updated on 17/Dec/18
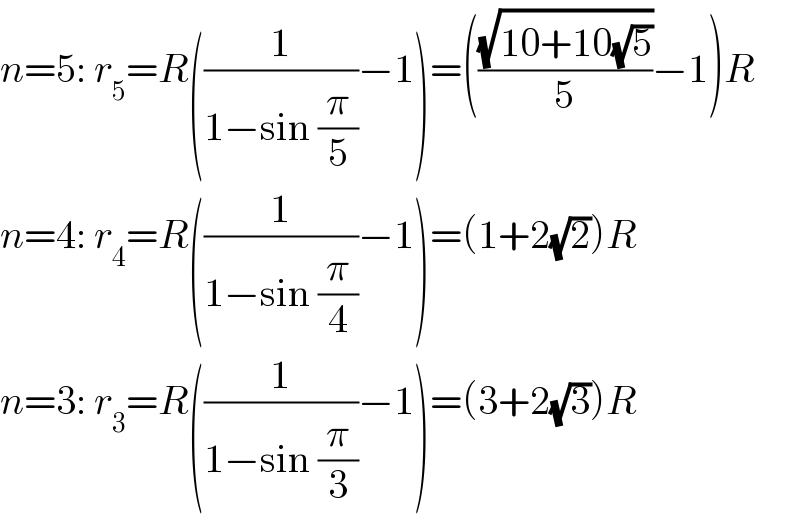
$${n}=\mathrm{5}:\:{r}_{\mathrm{5}} ={R}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{\mathrm{5}}}−\mathrm{1}\right)=\left(\frac{\sqrt{\mathrm{10}+\mathrm{10}\sqrt{\mathrm{5}}}}{\mathrm{5}}−\mathrm{1}\right){R} \\ $$$${n}=\mathrm{4}:\:{r}_{\mathrm{4}} ={R}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}−\mathrm{1}\right)=\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\right){R} \\ $$$${n}=\mathrm{3}:\:{r}_{\mathrm{3}} ={R}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{\mathrm{3}}}−\mathrm{1}\right)=\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right){R} \\ $$
Commented by ajfour last updated on 17/Dec/18
$${next}\:{LAYER}\:\:{Circles},\:{Sir}\:? \\ $$
Commented by mr W last updated on 18/Dec/18
![let s=radius of circles from next layer (√((s+r)^2 −s^2 ))+R+r=(s/(tan θ))=(s/(tan (π/n))) (√(r(2s+r)))=(s/(tan (π/n)))−R−r (s^2 /(tan^2 (π/n)))−2[(((R+r))/(tan (π/n)))+r]s+R(R+2r)=0 s=(((((R+r))/(tan (π/n)))+r+(√([(((R+r))/(tan (π/n)))+r]^2 −((R(R+2r))/(tan^2 (π/n))))))/(1/(tan^2 (π/n)))) ⇒s=tan (π/n) {R+(1+tan (π/n))r+(√([R+(1+tan (π/n))r]^2 −R(R+2r)))}](https://www.tinkutara.com/question/Q50602.png)
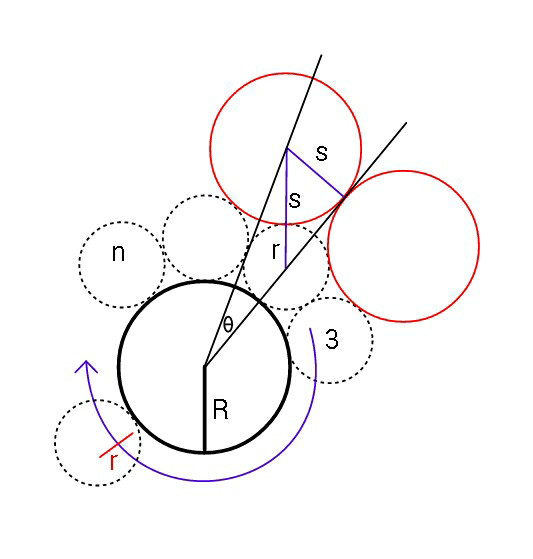
$${let}\:{s}={radius}\:{of}\:{circles}\:{from}\:{next}\:{layer} \\ $$$$\sqrt{\left({s}+{r}\right)^{\mathrm{2}} −{s}^{\mathrm{2}} }+{R}+{r}=\frac{{s}}{\mathrm{tan}\:\theta}=\frac{{s}}{\mathrm{tan}\:\frac{\pi}{{n}}} \\ $$$$\sqrt{{r}\left(\mathrm{2}{s}+{r}\right)}=\frac{{s}}{\mathrm{tan}\:\frac{\pi}{{n}}}−{R}−{r} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \:\frac{\pi}{{n}}}−\mathrm{2}\left[\frac{\left({R}+{r}\right)}{\mathrm{tan}\:\frac{\pi}{{n}}}+{r}\right]{s}+{R}\left({R}+\mathrm{2}{r}\right)=\mathrm{0} \\ $$$${s}=\frac{\frac{\left({R}+{r}\right)}{\mathrm{tan}\:\frac{\pi}{{n}}}+{r}+\sqrt{\left[\frac{\left({R}+{r}\right)}{\mathrm{tan}\:\frac{\pi}{{n}}}+{r}\right]^{\mathrm{2}} −\frac{{R}\left({R}+\mathrm{2}{r}\right)}{\mathrm{tan}^{\mathrm{2}} \:\frac{\pi}{{n}}}}}{\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\frac{\pi}{{n}}}} \\ $$$$\Rightarrow{s}=\mathrm{tan}\:\frac{\pi}{{n}}\:\left\{{R}+\left(\mathrm{1}+\mathrm{tan}\:\frac{\pi}{{n}}\right){r}+\sqrt{\left[{R}+\left(\mathrm{1}+\mathrm{tan}\:\frac{\pi}{{n}}\right){r}\right]^{\mathrm{2}} −{R}\left({R}+\mathrm{2}{r}\right)}\right\} \\ $$
Commented by ajfour last updated on 17/Dec/18
$${Heights}!\:{so}\:{quick}\:{sir},\:{some}\:{typos}, \\ $$$${i}\:{guess}.. \\ $$
Commented by ajfour last updated on 17/Dec/18
Commented by mr W last updated on 17/Dec/18
$${no}!\:{not}\:{such}\:{an}\:{integer}\:{n}\:{exists}. \\ $$$${n}\approx\mathrm{8}.\mathrm{84} \\ $$
Commented by ajfour last updated on 17/Dec/18

$${thanks}\:{sir}. \\ $$
Answered by Smail last updated on 18/Dec/18
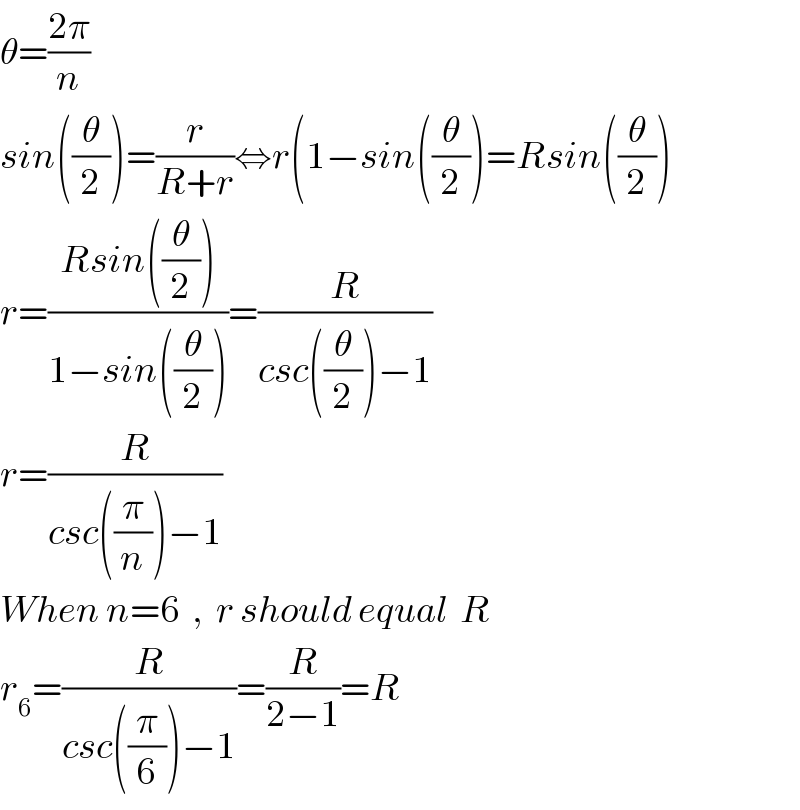
$$\theta=\frac{\mathrm{2}\pi}{{n}} \\ $$$${sin}\left(\frac{\theta}{\mathrm{2}}\right)=\frac{{r}}{{R}+{r}}\Leftrightarrow{r}\left(\mathrm{1}−{sin}\left(\frac{\theta}{\mathrm{2}}\right)={Rsin}\left(\frac{\theta}{\mathrm{2}}\right)\right. \\ $$$${r}=\frac{{Rsin}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−{sin}\left(\frac{\theta}{\mathrm{2}}\right)}=\frac{{R}}{{csc}\left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{1}} \\ $$$${r}=\frac{{R}}{{csc}\left(\frac{\pi}{{n}}\right)−\mathrm{1}} \\ $$$${When}\:{n}=\mathrm{6}\:\:,\:\:{r}\:{should}\:{equal}\:\:{R} \\ $$$${r}_{\mathrm{6}} =\frac{{R}}{{csc}\left(\frac{\pi}{\mathrm{6}}\right)−\mathrm{1}}=\frac{{R}}{\mathrm{2}−\mathrm{1}}={R} \\ $$
Commented by Smail last updated on 18/Dec/18
Commented by Smail last updated on 18/Dec/18
Commented by Smail last updated on 18/Dec/18

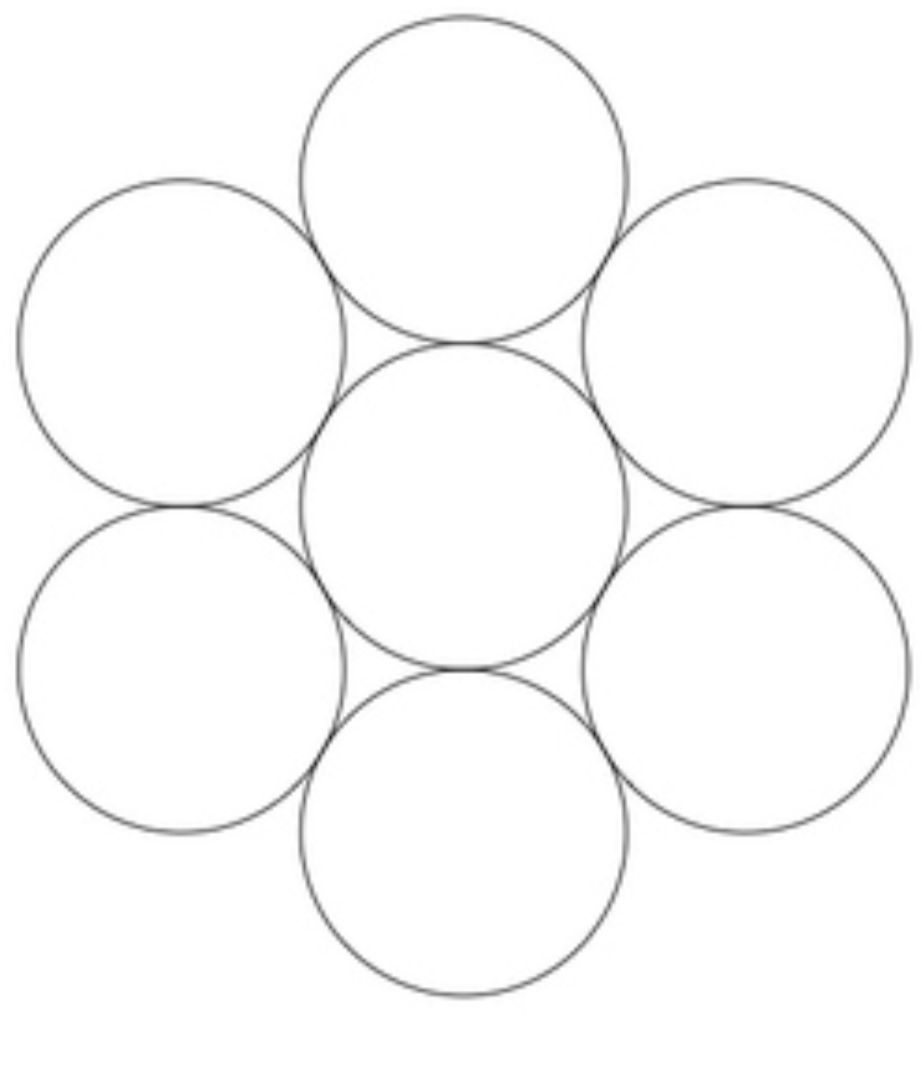
$${n}=\mathrm{6}\:\:{so}\:{r}={R} \\ $$
