Question Number 181766 by HeferH last updated on 30/Nov/22
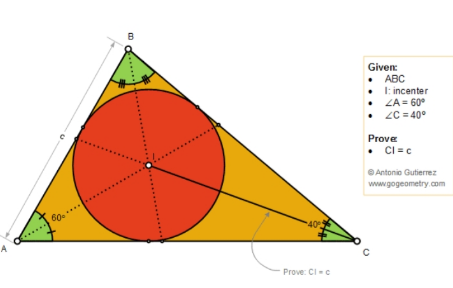
Answered by som(math1967) last updated on 30/Nov/22
![let radius of inner circle =r ((CI)/r)=cosec20⇒CI=rcosec20 c=rcot30+rcot40 =r(((cos30sin40+cos40sin30)/(sin30sin40))) =r(((2sin70)/(2sin20cos20))) =r[((cos(90−70))/(sin20cos20))]=rcosec20=CI ∴CI=c (proved)](https://www.tinkutara.com/question/Q181768.png)
$$\:{let}\:{radius}\:{of}\:{inner}\:{circle}\:={r} \\ $$$$\:\frac{{CI}}{{r}}={cosec}\mathrm{20}\Rightarrow{CI}={rcosec}\mathrm{20} \\ $$$$\:{c}={rcot}\mathrm{30}+{rcot}\mathrm{40} \\ $$$$={r}\left(\frac{{cos}\mathrm{30}{sin}\mathrm{40}+{cos}\mathrm{40}{sin}\mathrm{30}}{{sin}\mathrm{30}{sin}\mathrm{40}}\right) \\ $$$$={r}\left(\frac{\mathrm{2}{sin}\mathrm{70}}{\mathrm{2}{sin}\mathrm{20}{cos}\mathrm{20}}\right) \\ $$$$={r}\left[\frac{{cos}\left(\mathrm{90}−\mathrm{70}\right)}{{sin}\mathrm{20}{cos}\mathrm{20}}\right]={rcosec}\mathrm{20}={CI} \\ $$$$\therefore{CI}={c}\:\left({proved}\right) \\ $$
