Menu Close

Solve-x-a-2-2c-2-b-c-x-b-2-2a-2-c-a-x-c-2-2b-2-a-b-0-

Tinku Tara 0 Comments
Pin




Question Number 182131 by Agnibhoo98 last updated on 04/Dec/22
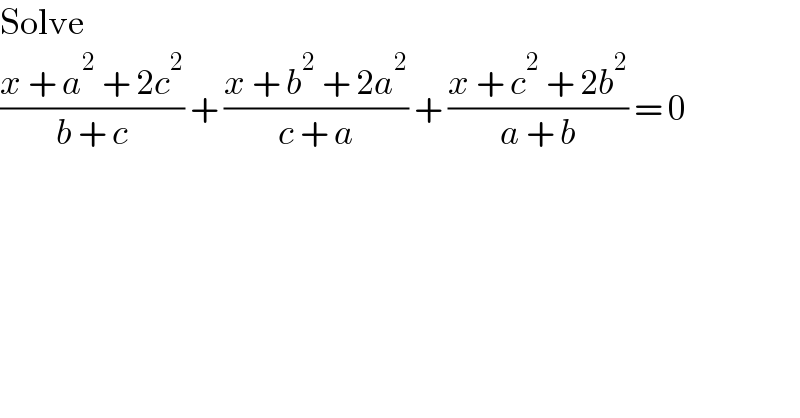
Solve ((x + a^2 + 2c^2 )/(b + c)) + ((x + b^2 + 2a^2 )/(c + a)) + ((x + c^2 + 2b^2 )/(a + b)) = 0
$$\mathrm{Solve} \\ $$$$\frac{{x}\:+\:{a}^{\mathrm{2}} \:+\:\mathrm{2}{c}^{\mathrm{2}} }{{b}\:+\:{c}}\:+\:\frac{{x}\:+\:{b}^{\mathrm{2}} \:+\:\mathrm{2}{a}^{\mathrm{2}} }{{c}\:+\:{a}}\:+\:\frac{{x}\:+\:{c}^{\mathrm{2}} \:+\:\mathrm{2}{b}^{\mathrm{2}} }{{a}\:+\:{b}}\:=\:\mathrm{0} \\ $$
Answered by manxsol last updated on 04/Dec/22
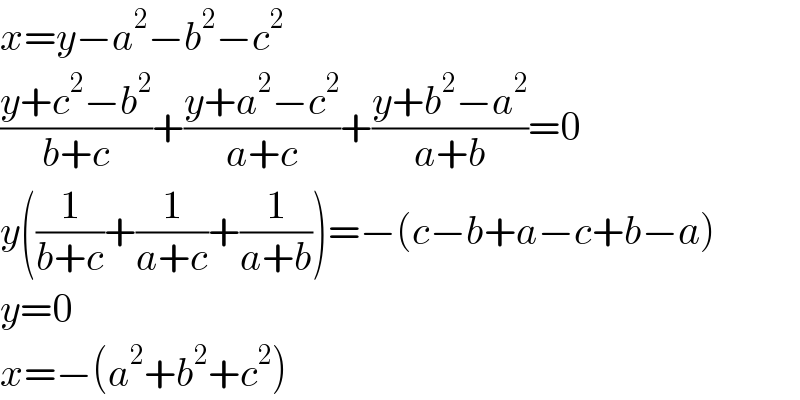
x=y−a^2 −b^2 −c^2 ((y+c^2 −b^2 )/(b+c))+((y+a^2 −c^2 )/(a+c))+((y+b^2 −a^2 )/(a+b))=0 y((1/(b+c))+(1/(a+c))+(1/(a+b)))=−(c−b+a−c+b−a) y=0 x=−(a^2 +b^2 +c^2 )
$${x}={y}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \\ $$$$\frac{{y}+{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}+{c}}+\frac{{y}+{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{a}+{c}}+\frac{{y}+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}+{b}}=\mathrm{0} \\ $$$${y}\left(\frac{\mathrm{1}}{{b}+{c}}+\frac{\mathrm{1}}{{a}+{c}}+\frac{\mathrm{1}}{{a}+{b}}\right)=−\left({c}−{b}+{a}−{c}+{b}−{a}\right) \\ $$$${y}=\mathrm{0} \\ $$$${x}=−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$
Answered by Rasheed.Sindhi last updated on 05/Dec/22
((x+a^2 +2c^2 )/(b+c))+((x+b^2 +2a^2 )/(c+a))+((x+c^2 +2b^2 )/(a+b))=0 ((x+a^2 +2c^2 )/(b+c))+(b−c) +((x+b^2 +2a^2 )/(c+a))+(c−a) +((x+c^2 +2b^2 )/(a+b))+(a−b)=0 [∵(b−c)+(c−a)+(a−b)=0] ((x+a^2 +2c^2 +b^2 −c^2 )/(b+c)) +((x+b^2 +2a^2 +c^2 −a^2 )/(c+a)) +((x+c^2 +2b^2 +a^2 −b^2 )/(a+b))=0 ((x+a^2 +b^2 +c^2 )/(b+c))+((x+a^2 +b^2 +c^2 )/(c+a))+((x+a^2 +b^2 +c^2 )/(a+b))=0 (x+a^2 +b^2 +c^2 )((1/(b+c))+(1/(c+a))+(1/(a+b)))=0 x+a^2 +b^2 +c^2 =0 x=−(a^2 +b^2 +c^2 )
$$\frac{{x}+{a}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} }{{b}+{c}}+\frac{{x}+{b}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} }{{c}+{a}}+\frac{{x}+{c}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} }{{a}+{b}}=\mathrm{0} \\ $$$$\frac{{x}+{a}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} }{{b}+{c}}+\left({b}−{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{x}+{b}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} }{{c}+{a}}+\left({c}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{x}+{c}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} }{{a}+{b}}+\left({a}−{b}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\because\left({b}−{c}\right)+\left({c}−{a}\right)+\left({a}−{b}\right)=\mathrm{0}\right] \\ $$$$\frac{{x}+{a}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}+{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{x}+{b}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{c}+{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{x}+{c}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}+{b}}=\mathrm{0} \\ $$$$\frac{{x}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{b}+{c}}+\frac{{x}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{c}+{a}}+\frac{{x}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{a}+{b}}=\mathrm{0} \\ $$$$\left({x}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}}{{b}+{c}}+\frac{\mathrm{1}}{{c}+{a}}+\frac{\mathrm{1}}{{a}+{b}}\right)=\mathrm{0} \\ $$$${x}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *