Question Number 70651 by sadimuhmud 136 last updated on 06/Oct/19
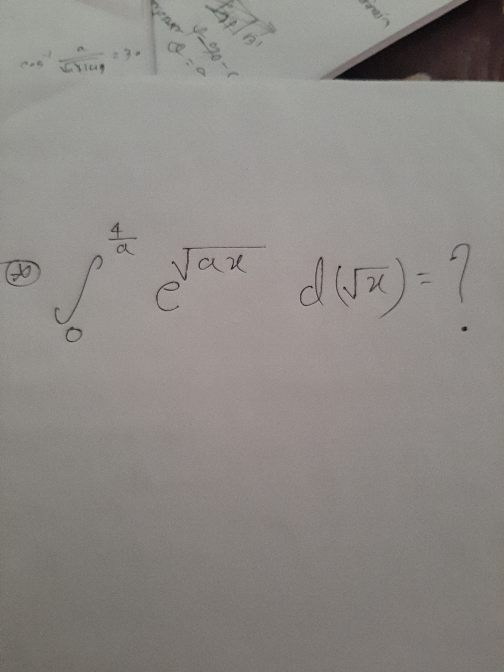
Commented by Prithwish sen last updated on 06/Oct/19
![Let (√x) = u ⇒ d((√x))=du ∫_0 ^(2/( (√a))) e^((√a)u) du = (1/( (√a))) [e^((√a)u) ]_0 ^(2/( (√a))) =(1/( (√a))) {e^2 −1} please check.](https://www.tinkutara.com/question/Q70656.png)
$$\mathrm{Let}\:\sqrt{\mathrm{x}}\:=\:\mathrm{u}\:\:\Rightarrow\:\mathrm{d}\left(\sqrt{\mathrm{x}}\right)=\mathrm{du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\:\sqrt{\mathrm{a}}}} \mathrm{e}^{\sqrt{\mathrm{a}}\mathrm{u}} \mathrm{du}\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\:\left[\boldsymbol{\mathrm{e}}^{\sqrt{\boldsymbol{\mathrm{a}}}\boldsymbol{\mathrm{u}}} \right]_{\mathrm{0}} ^{\frac{\mathrm{2}}{\:\sqrt{\boldsymbol{\mathrm{a}}}}} \:=\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{a}}}}\:\left\{\boldsymbol{\mathrm{e}}^{\mathrm{2}} −\mathrm{1}\right\} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by sadimuhmud 136 last updated on 06/Oct/19

$${thanks}.. \\ $$
Commented by Abdo msup. last updated on 06/Oct/19
![let (√x) =t ⇒d((√x))=dt and x=t^2 ⇒ ∫_0 ^(4/a) e^(√(ax)) d((√x)) =∫_0 ^(2/( (√a))) e^(√(at^2 )) dt =∫_0 ^(2/( (√a))) e^((√a)t) dt =[(1/( (√a))) e^((√a)t) ]_0 ^(2/( (√a))) =(1/( (√a))){ e^2 −1}](https://www.tinkutara.com/question/Q70680.png)
$${let}\:\sqrt{{x}}\:={t}\:\Rightarrow{d}\left(\sqrt{{x}}\right)={dt}\:\:{and}\:{x}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{4}}{{a}}} \:\:\:{e}^{\sqrt{{ax}}} {d}\left(\sqrt{{x}}\right)\:=\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\:\sqrt{{a}}}} \:\:\:{e}^{\sqrt{{at}^{\mathrm{2}} }} \:\:{dt}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\:\sqrt{{a}}}} \:\:\:{e}^{\sqrt{{a}}{t}} \:\:{dt} \\ $$$$=\left[\frac{\mathrm{1}}{\:\sqrt{{a}}}\:{e}^{\sqrt{{a}}{t}} \right]_{\mathrm{0}} ^{\frac{\mathrm{2}}{\:\sqrt{{a}}}} \:=\frac{\mathrm{1}}{\:\sqrt{{a}}}\left\{\:{e}^{\mathrm{2}} −\mathrm{1}\right\} \\ $$
