Question Number 117841 by john santu last updated on 14/Oct/20
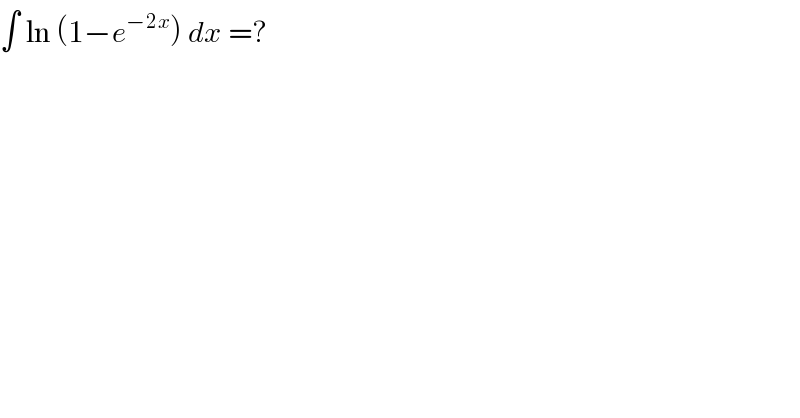
$$\int\:\mathrm{ln}\:\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right)\:{dx}\:=? \\ $$
Answered by MJS_new last updated on 14/Oct/20
![∫ln (1−e^(−2x) ) dx= [t=e^(−2x) → dx=−(e^(2x) /2)dt] =−(1/2)∫((ln (1−t))/t)dt=(1/2)Li_2 t =(1/2)Li_2 e^(−2x) +C](https://www.tinkutara.com/question/Q117846.png)
$$\int\mathrm{ln}\:\left(\mathrm{1}−\mathrm{e}^{−\mathrm{2}{x}} \right)\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{−\mathrm{2}{x}} \:\rightarrow\:{dx}=−\frac{\mathrm{e}^{\mathrm{2}{x}} }{\mathrm{2}}{dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)}{{t}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:{t}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:\mathrm{e}^{−\mathrm{2}{x}} \:+{C} \\ $$
Commented by john santu last updated on 14/Oct/20

$${thank}\:{prof} \\ $$
