Question Number 117863 by aurpeyz last updated on 14/Oct/20
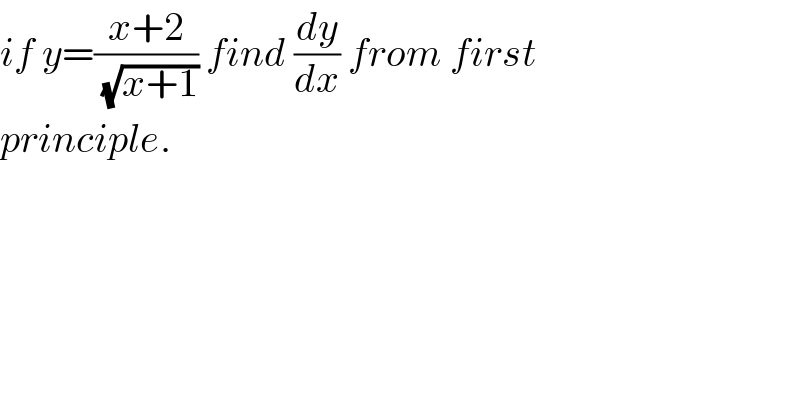
$${if}\:{y}=\frac{{x}+\mathrm{2}}{\:\sqrt{{x}+\mathrm{1}}}\:{find}\:\frac{{dy}}{{dx}}\:{from}\:{first} \\ $$$${principle}. \\ $$
Answered by bemath last updated on 14/Oct/20
![y=((x+1+1)/( (√(x+1)))) = (√(x+1)) +(1/( (√(x+1)))) (dy/dx) = lim_(h→0) (((√(x+h+1)) + (1/( (√(x+h+1))))−(√(x+1)) −(1/( (√(x+1)))))/h) =lim_(h→0) (h/(h((√(x+h+1))+(√(x+1))))) +lim_(h→0) (((1/( (√(x+h+1))))−(1/( (√(x+1)))))/h) = (1/(2(√(x+1)))) + lim_(h→0) (((√(x+1))−(√(x+h+1)))/(h((√((x+1)(x+h+1))))) =(1/(2(√(x+1)))) + (1/(x+1)) .lim_(x→0) ((−h)/(h((√(x+h+1))+(√(x+1))))) = (1/(2(√(x+1)))) −(1/(x+1)).(1/(2(√(x+1)))) =(1/(2(√(x+1)))) [1−(1/(x+1)) ] = (x/(2(x+1)^(3/2) )) or (x/(2(x+1)(√(x+1))))](https://www.tinkutara.com/question/Q117867.png)
$$\mathrm{y}=\frac{\mathrm{x}+\mathrm{1}+\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}}\:=\:\sqrt{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{h}+\mathrm{1}}}−\sqrt{\mathrm{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}}}{\mathrm{h}} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{h}}{\mathrm{h}\left(\sqrt{\mathrm{x}+\mathrm{h}+\mathrm{1}}+\sqrt{\mathrm{x}+\mathrm{1}}\right)}\:+\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{h}+\mathrm{1}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}}}{\mathrm{h}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}\:+\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}+\mathrm{h}+\mathrm{1}}}{\mathrm{h}\left(\sqrt{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{h}+\mathrm{1}\right)}\right.} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}\:+\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{h}}{\mathrm{h}\left(\sqrt{\mathrm{x}+\mathrm{h}+\mathrm{1}}+\sqrt{\mathrm{x}+\mathrm{1}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}\:−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}\:\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\right]\:=\:\frac{\mathrm{x}}{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\mathrm{or}\:\frac{\mathrm{x}}{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}+\mathrm{1}}} \\ $$
