Menu Close

0-x-2-f-2t-3-t-2-6-dt-ln-x-then-f-106-

Tinku Tara 0 Comments
Pin




Question Number 183450 by cortano1 last updated on 26/Dec/22
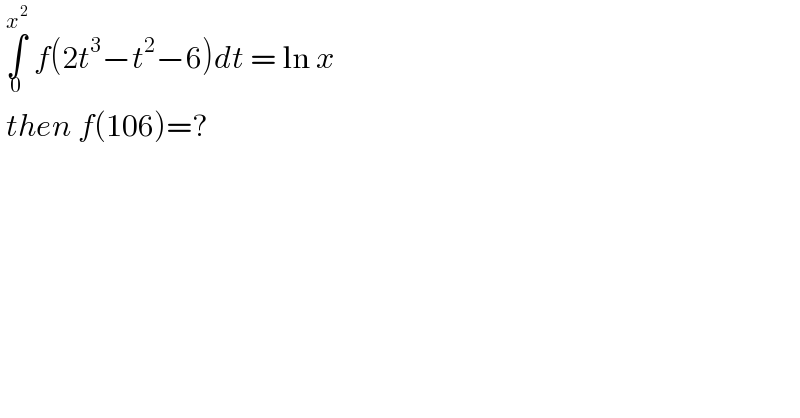
∫_0 ^x^2 f(2t^3 −t^2 −6)dt = ln x then f(106)=?
$$\:\underset{\mathrm{0}} {\overset{{x}^{\mathrm{2}} } {\int}}\:{f}\left(\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{6}\right){dt}\:=\:\mathrm{ln}\:{x}\: \\ $$$$\:{then}\:{f}\left(\mathrm{106}\right)=? \\ $$
Answered by mahdipoor last updated on 26/Dec/22
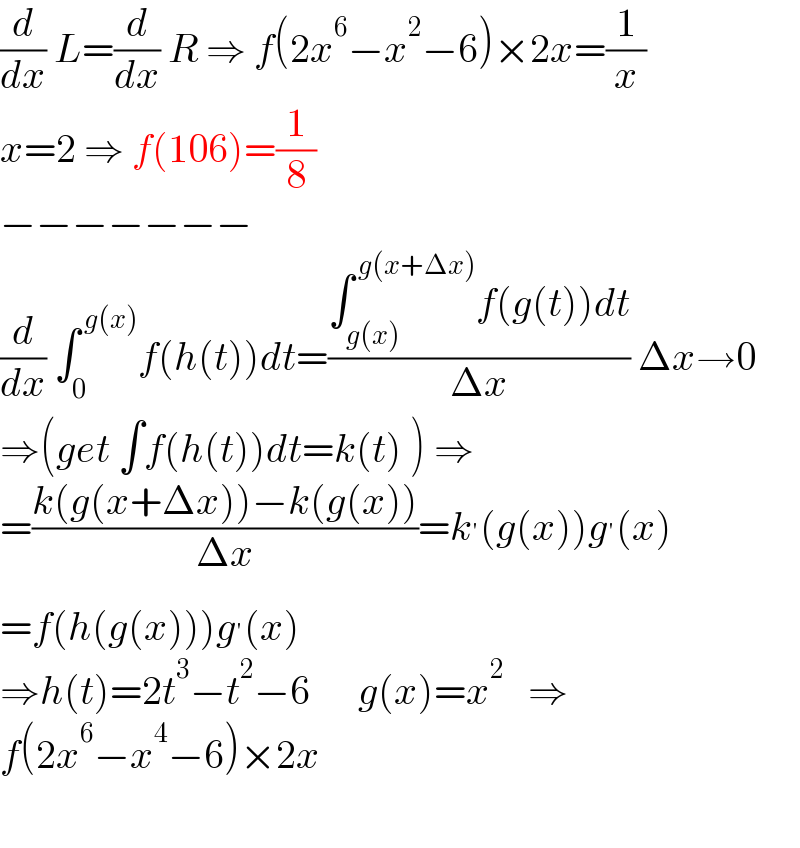
(d/dx) L=(d/dx) R ⇒ f(2x^6 −x^2 −6)×2x=(1/x) x=2 ⇒ f(106)=(1/8) −−−−−−− (d/dx) ∫_0 ^( g(x)) f(h(t))dt=((∫_(g(x)) ^( g(x+Δx)) f(g(t))dt)/(Δx)) Δx→0 ⇒(get ∫f(h(t))dt=k(t) ) ⇒ =((k(g(x+Δx))−k(g(x)))/(Δx))=k^′ (g(x))g^′ (x) =f(h(g(x)))g^′ (x) ⇒h(t)=2t^3 −t^2 −6 g(x)=x^2 ⇒ f(2x^6 −x^4 −6)×2x
$$\frac{{d}}{{dx}}\:{L}=\frac{{d}}{{dx}}\:{R}\:\Rightarrow\:{f}\left(\mathrm{2}{x}^{\mathrm{6}} −{x}^{\mathrm{2}} −\mathrm{6}\right)×\mathrm{2}{x}=\frac{\mathrm{1}}{{x}} \\ $$$${x}=\mathrm{2}\:\Rightarrow\:{f}\left(\mathrm{106}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$−−−−−−− \\ $$$$\frac{{d}}{{dx}}\:\int_{\mathrm{0}} ^{\:{g}\left({x}\right)} {f}\left({h}\left({t}\right)\right){dt}=\frac{\int_{{g}\left({x}\right)} ^{\:{g}\left({x}+\Delta{x}\right)} {f}\left({g}\left({t}\right)\right){dt}}{\Delta{x}}\:\Delta{x}\rightarrow\mathrm{0} \\ $$$$\Rightarrow\left({get}\:\int{f}\left({h}\left({t}\right)\right){dt}={k}\left({t}\right)\:\right)\:\Rightarrow \\ $$$$=\frac{{k}\left({g}\left({x}+\Delta{x}\right)\right)−{k}\left({g}\left({x}\right)\right)}{\Delta{x}}={k}^{'} \left({g}\left({x}\right)\right){g}^{'} \left({x}\right) \\ $$$$={f}\left({h}\left({g}\left({x}\right)\right)\right){g}^{'} \left({x}\right) \\ $$$$\Rightarrow{h}\left({t}\right)=\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{6}\:\:\:\:\:\:{g}\left({x}\right)={x}^{\mathrm{2}} \:\:\:\Rightarrow \\ $$$${f}\left(\mathrm{2}{x}^{\mathrm{6}} −{x}^{\mathrm{4}} −\mathrm{6}\right)×\mathrm{2}{x} \\ $$$$ \\ $$
Answered by mr W last updated on 26/Dec/22
say f(2t^3 −t^2 −6)=g(t) ∫_0 ^x^2 g(t)dt=ln x (d/dx)[∫_0 ^x^2 g(t)dt]=(d/dx)(ln x) g(x^2 )(2x)=(1/x) ⇒g(x^2 )=(1/(2x^2 )) ⇒g(t)=(1/(2t)) ⇒f(2t^3 −t^2 −6)=(1/(2t)) set 2t^3 −t^2 −6=106 2t^3 −t^2 −112=0 (t−4)(2t^2 +7t+28)=0 ⇒t=4 ⇒f(106)=(1/(2×4))=(1/8) ✓
$${say}\:{f}\left(\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{6}\right)={g}\left({t}\right) \\ $$$$\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} } {g}\left({t}\right){dt}=\mathrm{ln}\:{x} \\ $$$$\frac{{d}}{{dx}}\left[\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} } {g}\left({t}\right){dt}\right]=\frac{{d}}{{dx}}\left(\mathrm{ln}\:{x}\right) \\ $$$${g}\left({x}^{\mathrm{2}} \right)\left(\mathrm{2}{x}\right)=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{g}\left({x}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{g}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}{t}} \\ $$$$\Rightarrow{f}\left(\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{6}\right)=\frac{\mathrm{1}}{\mathrm{2}{t}} \\ $$$${set}\:\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{6}=\mathrm{106} \\ $$$$\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{112}=\mathrm{0} \\ $$$$\left({t}−\mathrm{4}\right)\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{7}{t}+\mathrm{28}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{4} \\ $$$$\Rightarrow{f}\left(\mathrm{106}\right)=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{8}}\:\checkmark \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *