Question Number 52609 by subhankar10 last updated on 10/Jan/19
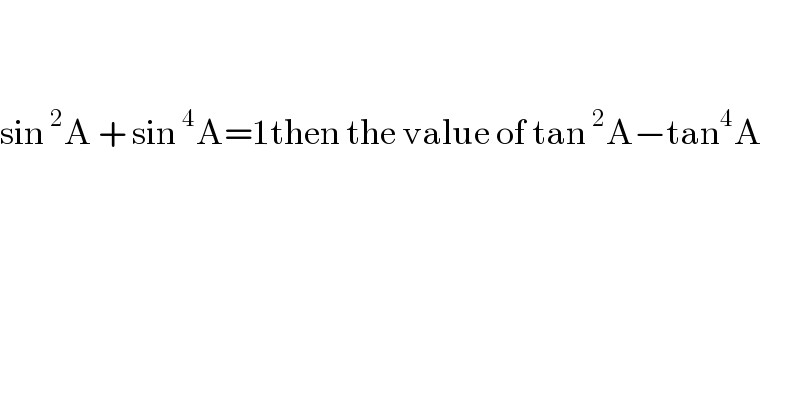
$$ \\ $$$$ \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}\:+\:\mathrm{sin}\:^{\mathrm{4}} \mathrm{A}=\mathrm{1then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}−\mathrm{tan}^{\mathrm{4}} \mathrm{A} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
![sin^4 A=1−sin^2 A sin^2 A×sin^2 A=cos^2 A tan^2 A=cosec^2 A tan^2 A−tan^4 A tan^2 A(1−tan^2 A) =cosec^2 A(1−cosec^2 A) =(1/(sin^2 A))(((sin^2 A−1)/(sin^2 A))) =((sin^2 A−sin^2 A−sin^4 A)/(sin^4 A))[since sin^2 A+sin^4 A=1] =−1](https://www.tinkutara.com/question/Q52615.png)
$${sin}^{\mathrm{4}} {A}=\mathrm{1}−{sin}^{\mathrm{2}} {A} \\ $$$${sin}^{\mathrm{2}} {A}×{sin}^{\mathrm{2}} {A}={cos}^{\mathrm{2}} {A} \\ $$$${tan}^{\mathrm{2}} {A}={cosec}^{\mathrm{2}} {A} \\ $$$${tan}^{\mathrm{2}} {A}−{tan}^{\mathrm{4}} {A} \\ $$$${tan}^{\mathrm{2}} {A}\left(\mathrm{1}−{tan}^{\mathrm{2}} {A}\right) \\ $$$$={cosec}^{\mathrm{2}} {A}\left(\mathrm{1}−{cosec}^{\mathrm{2}} {A}\right) \\ $$$$=\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {A}}\left(\frac{{sin}^{\mathrm{2}} {A}−\mathrm{1}}{{sin}^{\mathrm{2}} {A}}\right) \\ $$$$=\frac{{sin}^{\mathrm{2}} {A}−{sin}^{\mathrm{2}} {A}−{sin}^{\mathrm{4}} {A}}{{sin}^{\mathrm{4}} {A}}\left[{since}\:{sin}^{\mathrm{2}} {A}+{sin}^{\mathrm{4}} {A}=\mathrm{1}\right] \\ $$$$=−\mathrm{1} \\ $$
