Question Number 52703 by maxmathsup by imad last updated on 11/Jan/19
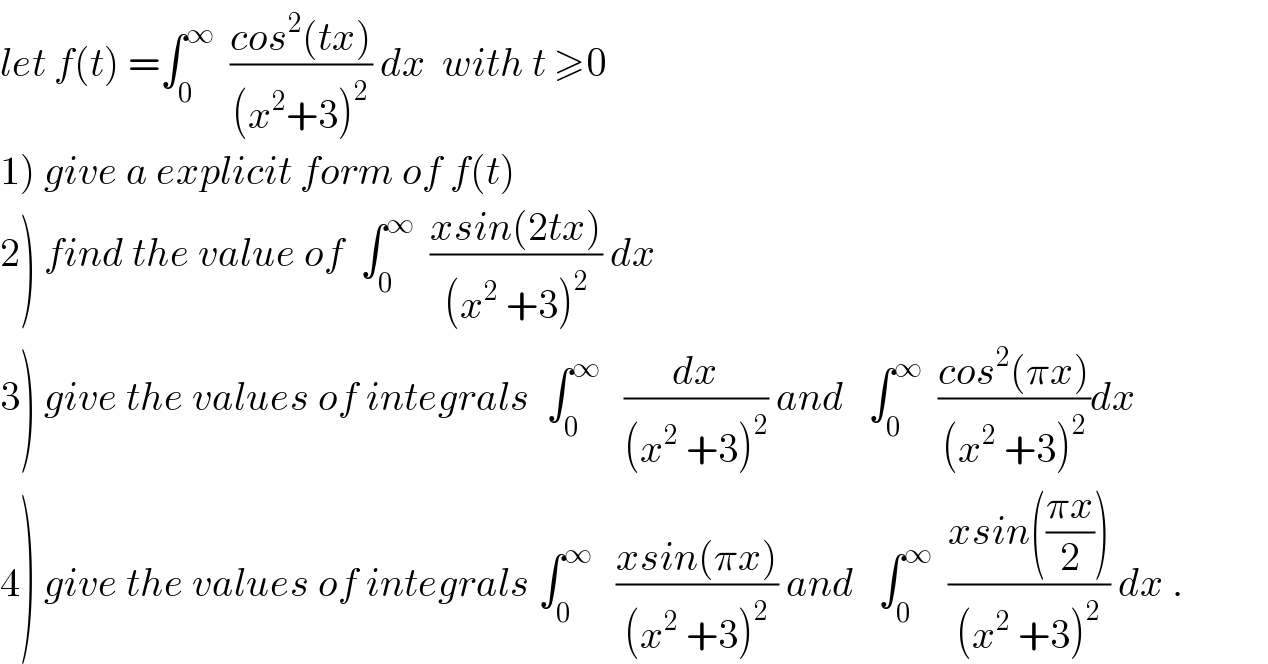
$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}^{\mathrm{2}} \left({tx}\right)}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\:{dx}\:\:{with}\:{t}\:\geqslant\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{give}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({t}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xsin}\left(\mathrm{2}{tx}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\left.\mathrm{3}\right)\:{give}\:{the}\:{values}\:{of}\:{integrals}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:{and}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}^{\mathrm{2}} \left(\pi{x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{4}\right)\:{give}\:{the}\:{values}\:{of}\:{integrals}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{xsin}\left(\pi{x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:{and}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xsin}\left(\frac{\pi{x}}{\mathrm{2}}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:{dx}\:. \\ $$
Commented by Abdo msup. last updated on 13/Jan/19
![channgement x=(√3)u give f(t)=∫_0 ^∞ ((cos^2 ((√3)tu))/(9(u^2 +1)^2 )) (√3)du =((√3)/9) ∫_0 ^(+∞) ((cos^2 ((√3)tu))/((u^2 +1)^2 )) du =((√3)/(18)) ∫_(−∞) ^(+∞) ((cos^2 ((√3)tu))/((u^2 +1)^2 ))du =((√3)/(18)) ∫_(−∞) ^(+∞) ((1+cos(2(√3)tu))/(2(u^2 +1)^2 ))du =((√3)/(36)) ∫_(−∞) ^(+∞) (du/((u^2 +1)^2 )) +((√3)/(36)) ∫_(−∞) ^(+∞) ((cos(2(√3)tu)du)/((u^2 +1)^2 )) ∫_(−∞) ^(+∞) (du/((u^2 +1)^2 )) =_(u=tanθ) ∫_(−(π/2)) ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ =2 ∫_0 ^(π/2) cos^2 θ dθ =2 ∫_0 ^(π/2) ((1+cos(2θ))/2) dθ =(π/2) +[(1/2)sin(2θ)]_0 ^(π/2) =(π/2) let determine ∫_(−∞) ^(+∞) ((cos(2(√3)tu))/((u^2 +1)^2 )) du =I I =Re( ∫_(−∞) ^(+∞) (e^(2i(√3)tu) /((u^2 +1)^2 )) du) let ϕ(z)= (e^(2i(√3)tz) /((z^2 +1)^2 )) ⇒ϕ(z)=(e^(2i(√3)tz) /((z−i)^2 (z+i)^2 )) the poles of ϕ are i and −i(doubles) so ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Re(ϕ,i) Res(ϕ,i)=lim_(z→i) (1/((2−1)!)){(z−i)^2 ϕ(z)}^((1)) =lim_(z→i) { (e^(2i(√3)t z) /((z+i)^2 ))}^((1)) =lim_(z→i) ((2i(√3)t e^(2i(√3)tz) (z+i)^2 −2(z+i)e^(2i(√3)tz) )/((z+i)^4 )) =lim_(z→i) (((2i(√3)t (z+i)−2)e^(2i(√3)tz) )/((z+i)^3 )) =(((2i(√3)t(2i)−2)e^(−2(√3)t) )/((2i)^3 )) =(((−4i(√3)t−2) e^(−2(√3)t) )/(−8i)) =(((2i(√3)t +1)e^(−2(√3)t) )/(4i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz= 2iπ (((2i(√3)t +1)e^(−2(√3)t) )/(4i)) =(π/2)(2i(√3)t +1)e^(−2(√3)t) but I =Re(∫_(−∞) ^(+∞) ϕ(z)dz) =(π/2) e^(−2(√3)t) ⇒ f(t)=((π(√3))/(72)) +((√3)/(36)){ (π/2) e^(−2(√3)t) } ⇒ f(t) =((π(√3))/(72))(1+e^(−2(√3)t) ) .](https://www.tinkutara.com/question/Q52816.png)
$${channgement}\:{x}=\sqrt{\mathrm{3}}{u}\:{give}\: \\ $$$${f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{tu}\right)}{\mathrm{9}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\sqrt{\mathrm{3}}{du} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{cos}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{tu}\right)}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{du}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\:\int_{−\infty} ^{+\infty} \:\frac{{cos}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{tu}\right)}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{1}+{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}{tu}\right)}{\mathrm{2}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{du}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}{tu}\right){du}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{du}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=_{{u}={tan}\theta} \:\:\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\:{d}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\:+\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:=\frac{\pi}{\mathrm{2}}\:\:{let}\:{determine}\: \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}{tu}\right)}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{du}\:={I} \\ $$$${I}\:={Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{tu}} }{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{du}\right)\:{let} \\ $$$$\varphi\left({z}\right)=\:\frac{{e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{tz}} }{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\varphi\left({z}\right)=\frac{{e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{tz}} }{\left({z}−{i}\right)^{\mathrm{2}} \left({z}+{i}\right)^{\mathrm{2}} } \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:{i}\:{and}\:−{i}\left({doubles}\right)\:{so} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Re}\left(\varphi,{i}\right) \\ $$$${Res}\left(\varphi,{i}\right)={lim}_{{z}\rightarrow{i}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{i}\right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \left\{\:\frac{{e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:{z}} }{\left({z}+{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:{e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{tz}} \left({z}+{i}\right)^{\mathrm{2}} \:−\mathrm{2}\left({z}+{i}\right){e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{tz}} }{\left({z}+{i}\right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:\left({z}+{i}\right)−\mathrm{2}\right){e}^{\mathrm{2}{i}\sqrt{\mathrm{3}}{tz}} }{\left({z}+{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\left(\mathrm{2}{i}\right)−\mathrm{2}\right){e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} }{\left(\mathrm{2}{i}\right)^{\mathrm{3}} }\:=\frac{\left(−\mathrm{4}{i}\sqrt{\mathrm{3}}{t}−\mathrm{2}\right)\:{e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} }{−\mathrm{8}{i}} \\ $$$$=\frac{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:+\mathrm{1}\right){e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} }{\mathrm{4}{i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}= \\ $$$$\mathrm{2}{i}\pi\:\frac{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:+\mathrm{1}\right){e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} }{\mathrm{4}{i}}\:=\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:+\mathrm{1}\right){e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} \:{but} \\ $$$${I}\:={Re}\left(\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\right)\:=\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} \:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{72}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left\{\:\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} \right\}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{72}}\left(\mathrm{1}+{e}^{−\mathrm{2}\sqrt{\mathrm{3}}{t}} \right)\:\:. \\ $$
