Question Number 118545 by I want to learn more last updated on 18/Oct/20

Commented by Tawa11 last updated on 15/Sep/21

$$\mathrm{nice} \\ $$
Answered by mr W last updated on 18/Oct/20
Commented by mr W last updated on 18/Oct/20
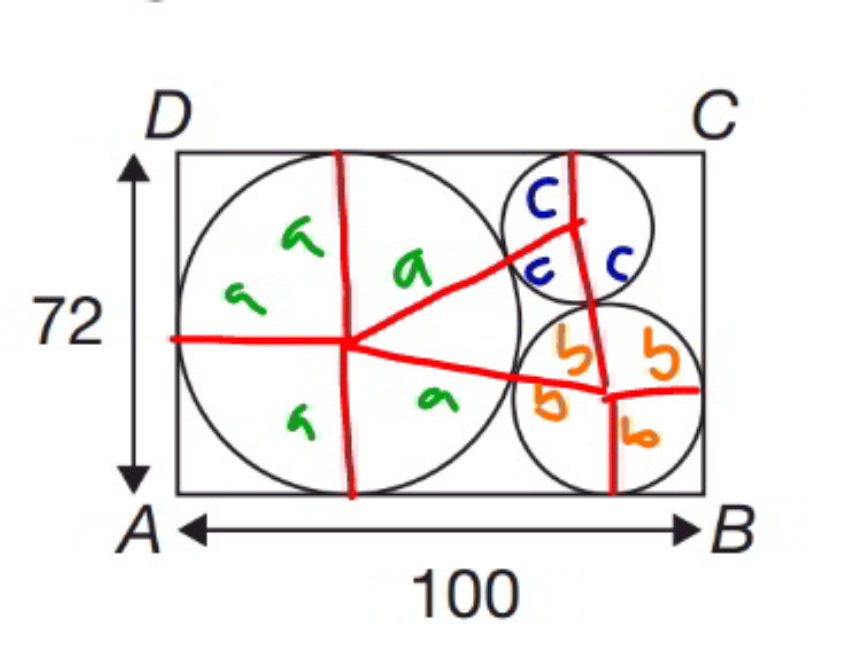
![a=((72)/2)=36 (a+b)^2 =(a−b)^2 +(100−a−b)^2 144b=(64−b)^2 64^2 −272b+b^2 =0 ⇒b=136±120 ⇒b=16 [100−a−b−(√((a+c)^2 −(a−c)^2 ))]^2 +(72−b−c)^2 =(b+c)^2 (48−12(√c))^2 +(56−c)^2 =(16+c)^2 48^2 −2×12×48(√c)+56^2 =16^2 9−2(√c)=0 ⇒c=((81)/4)](https://www.tinkutara.com/question/Q118565.png)
$${a}=\frac{\mathrm{72}}{\mathrm{2}}=\mathrm{36} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} =\left({a}−{b}\right)^{\mathrm{2}} +\left(\mathrm{100}−{a}−{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{144}{b}=\left(\mathrm{64}−{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{64}^{\mathrm{2}} −\mathrm{272}{b}+{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{b}=\mathrm{136}\pm\mathrm{120}\:\Rightarrow{b}=\mathrm{16} \\ $$$$\left[\mathrm{100}−{a}−{b}−\sqrt{\left({a}+{c}\right)^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} +\left(\mathrm{72}−{b}−{c}\right)^{\mathrm{2}} =\left({b}+{c}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{48}−\mathrm{12}\sqrt{{c}}\right)^{\mathrm{2}} +\left(\mathrm{56}−{c}\right)^{\mathrm{2}} =\left(\mathrm{16}+{c}\right)^{\mathrm{2}} \\ $$$$\mathrm{48}^{\mathrm{2}} −\mathrm{2}×\mathrm{12}×\mathrm{48}\sqrt{{c}}+\mathrm{56}^{\mathrm{2}} =\mathrm{16}^{\mathrm{2}} \\ $$$$\mathrm{9}−\mathrm{2}\sqrt{{c}}=\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{\mathrm{81}}{\mathrm{4}} \\ $$
Commented by I want to learn more last updated on 25/Oct/20
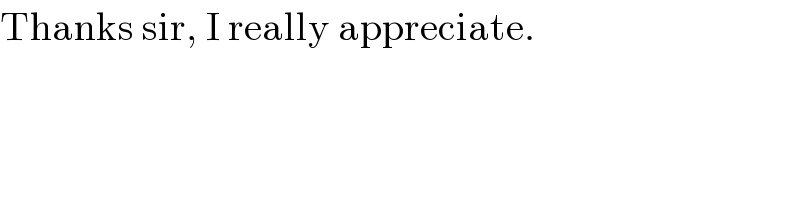
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
