Menu Close

Question-118710

Tinku Tara 0 Comments
Pin




Question Number 118710 by eric last updated on 19/Oct/20
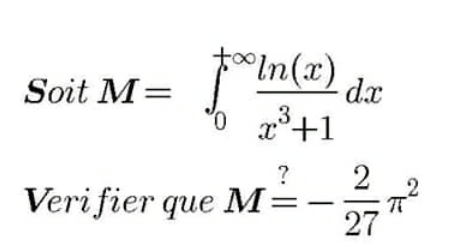
Answered by mathmax by abdo last updated on 19/Oct/20
M=∫_0 ^∞ ((lnx)/(1+x^3 ))dx =∫_0 ^1 ((lnx)/(1+x^3 ))dx +∫_1 ^∞ ((lnx)/(1+x^3 ))dx(→x=(1/t)) =∫_0 ^1 ((lnx)/(1+x^3 ))dx −∫_0 ^1 ((−lnt)/(1+(1/t^3 )))×(((−dt)/t^2 )) =∫_0 ^1 ((lnx)/(1+x^3 ))dx−∫_0 ^1 ((tlnt)/(1+t^3 )) dt we have ∫_0 ^1 ((lnx)/(1+x^3 ))dx =∫_0 ^1 lnxΣ_(n=0) ^∞ (−1)^n x^(3n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n) lnx dx U_n =∫_0 ^1 x^(3n) lnxdx =_(byparts) [(x^(3n+1) /(3n+1))lnx]_0 ^1 −∫_0 ^1 (x^(3n) /(3n+1))dx =−(1/((3n+1)^2 )) ⇒∫_0 ^1 ((lnx)/(1+x^3 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) ∫_0 ^1 ((xlnx)/(1+x^3 ))dx =∫_0 ^1 xlnxΣ_(n=0) ^∞ (−1)^n x^(3n) dx=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n+1) lnx dx V_n =∫_0 ^1 x^(3n+1) lnx dx =[(x^(3n+2) /(3n+2))lnx]_0 ^1 −∫_0 ^1 (x^(3n+1) /(3n+2))dx =−(1/((3n+2)^2 )) ⇒∫_0 ^1 ((xlnx)/(1+x^3 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((3n+2)^2 )) ⇒ M =−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) +Σ_(n=0) ^∞ (((−1)^n )/((3n+2)^2 )) rest calculus of those series ...be continued...
$$\mathrm{M}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\left(\rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{lnt}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }}×\left(\frac{−\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{tlnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{3}} }\:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{lnx}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{3n}} \mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{3n}} \mathrm{lnx}\:\mathrm{dx} \\ $$$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{3n}} \mathrm{lnxdx}\:=_{\mathrm{byparts}} \:\:\:\left[\frac{\mathrm{x}^{\mathrm{3n}+\mathrm{1}} }{\mathrm{3n}+\mathrm{1}}\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{3n}} }{\mathrm{3n}+\mathrm{1}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{3n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{3n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xlnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xlnx}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{3n}} \mathrm{dx}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{3n}+\mathrm{1}} \mathrm{lnx}\:\mathrm{dx} \\ $$$$\mathrm{V}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{3n}+\mathrm{1}} \mathrm{lnx}\:\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{3n}+\mathrm{2}} }{\mathrm{3n}+\mathrm{2}}\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{3n}+\mathrm{1}} }{\mathrm{3n}+\mathrm{2}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{3n}+\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xlnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{3n}+\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{M}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{3n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{3n}+\mathrm{2}\right)^{\mathrm{2}} }\:\:\mathrm{rest}\:\mathrm{calculus}\:\mathrm{of}\:\mathrm{those} \\ $$$$\mathrm{series}\:…\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by mathdave last updated on 19/Oct/20
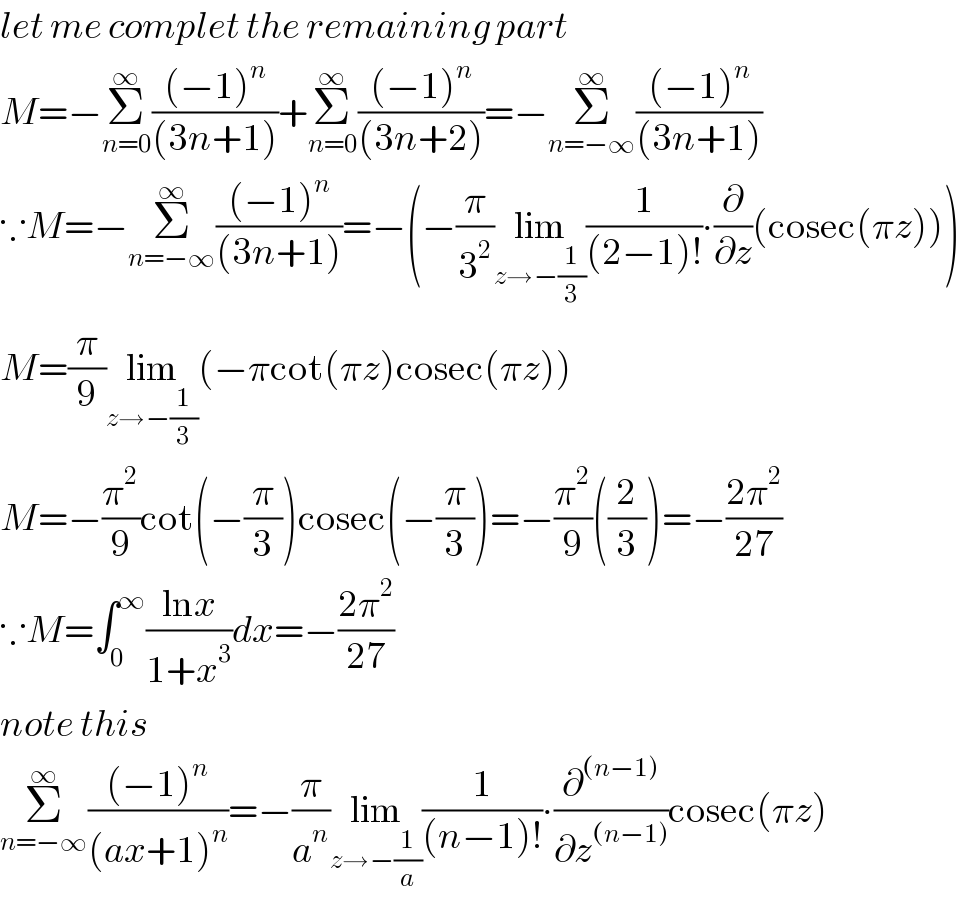
let me complet the remaining part M=−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)))+Σ_(n=0) ^∞ (((−1)^n )/((3n+2)))=−Σ_(n=−∞) ^∞ (((−1)^n )/((3n+1))) ∵M=−Σ_(n=−∞) ^∞ (((−1)^n )/((3n+1)))=−(−(π/3^2 )lim_(z→−(1/3)) (1/((2−1)!))∙(∂/∂z)(cosec(πz))) M=(π/9)lim_(z→−(1/3)) (−πcot(πz)cosec(πz)) M=−(π^2 /9)cot(−(π/3))cosec(−(π/3))=−(π^2 /9)((2/3))=−((2π^2 )/(27)) ∵M=∫_0 ^∞ ((lnx)/(1+x^3 ))dx=−((2π^2 )/(27)) note this Σ_(n=−∞) ^∞ (((−1)^n )/((ax+1)^n ))=−(π/a^n )lim_(z→−(1/a)) (1/((n−1)!))∙(∂^((n−1)) /∂z^((n−1)) )cosec(πz)
$${let}\:{me}\:{complet}\:{the}\:{remaining}\:{part} \\ $$$${M}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{3}{n}+\mathrm{2}\right)}=−\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$$$\because{M}=−\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)}=−\left(−\frac{\pi}{\mathrm{3}^{\mathrm{2}} }\underset{{z}\rightarrow−\frac{\mathrm{1}}{\mathrm{3}}} {\mathrm{lim}}\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\centerdot\frac{\partial}{\partial{z}}\left(\mathrm{cosec}\left(\pi{z}\right)\right)\right) \\ $$$${M}=\frac{\pi}{\mathrm{9}}\underset{{z}\rightarrow−\frac{\mathrm{1}}{\mathrm{3}}} {\mathrm{lim}}\left(−\pi\mathrm{cot}\left(\pi{z}\right)\mathrm{cosec}\left(\pi{z}\right)\right) \\ $$$${M}=−\frac{\pi^{\mathrm{2}} }{\mathrm{9}}\mathrm{cot}\left(−\frac{\pi}{\mathrm{3}}\right)\mathrm{cosec}\left(−\frac{\pi}{\mathrm{3}}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{9}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=−\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{27}} \\ $$$$\because{M}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx}=−\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{27}}\:\: \\ $$$${note}\:{this} \\ $$$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({ax}+\mathrm{1}\right)^{{n}} }=−\frac{\pi}{{a}^{{n}} }\underset{{z}\rightarrow−\frac{\mathrm{1}}{{a}}} {\mathrm{lim}}\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\centerdot\frac{\partial^{\left({n}−\mathrm{1}\right)} }{\partial{z}^{\left({n}−\mathrm{1}\right)} }\mathrm{cosec}\left(\pi{z}\right) \\ $$
Answered by mnjuly1970 last updated on 19/Oct/20
assume: f(a)=∫_0 ^( ∞) (x^a /(1+x^3 ))dx goal : M=f ′(0)=? euler reflection formula... f (a)=^(x^3 =t) (1/3)∫_0 ^( ∞) (t^((((a−2)/3)+1)−1) /(1+t))dt=(1/3)β(((a+1)/3) ,1−((a+1)/3)) =(1/3)Γ(((a+1)/3))Γ(1−((a+1)/3)) =(1/3)∗(π/(sin((π/3)+((πa)/3)))) ∴ f ′(a)=(π/3)∗((−(π/3)cos((π/3)+((πa)/3)))/(sin^2 ((π/3)+((πa)/3)))) ∴ M=f ′(0)=((−π^2 )/9)∗((1/2)/(3/4)) = −((2π^2 )/(27)) ✓ ...m.n.1970...
$$\:{assume}:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{a}} }{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$$$\:\:\:\:\:{goal}\::\:{M}={f}\:'\left(\mathrm{0}\right)=? \\ $$$$\:\:\:{euler}\:{reflection} \\ $$$${formula}… \\ $$$$\:\:{f}\:\left({a}\right)\overset{{x}^{\mathrm{3}} ={t}} {=}\:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\infty} \:\frac{{t}^{\left(\frac{{a}−\mathrm{2}}{\mathrm{3}}+\mathrm{1}\right)−\mathrm{1}} }{\mathrm{1}+{t}}{dt}=\frac{\mathrm{1}}{\mathrm{3}}\beta\left(\frac{{a}+\mathrm{1}}{\mathrm{3}}\:,\mathrm{1}−\frac{{a}+\mathrm{1}}{\mathrm{3}}\right)\:\:\:\:\: \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\mathrm{1}−\frac{{a}+\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\left.\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\ast\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}+\frac{\pi{a}}{\mathrm{3}}\right.}\right) \\ $$$$\:\:\:\:\:\therefore\:\:{f}\:'\left({a}\right)=\frac{\pi}{\mathrm{3}}\ast\frac{−\frac{\pi}{\mathrm{3}}{cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\pi{a}}{\mathrm{3}}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}+\frac{\pi{a}}{\mathrm{3}}\right)} \\ $$$$\:\:\:\:\therefore\:{M}={f}\:'\left(\mathrm{0}\right)=\frac{−\pi^{\mathrm{2}} }{\mathrm{9}}\ast\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{3}}{\mathrm{4}}}\:=\:−\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{27}}\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{m}.{n}.\mathrm{1970}… \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *