Question Number 53462 by maxmathsup by imad last updated on 22/Jan/19
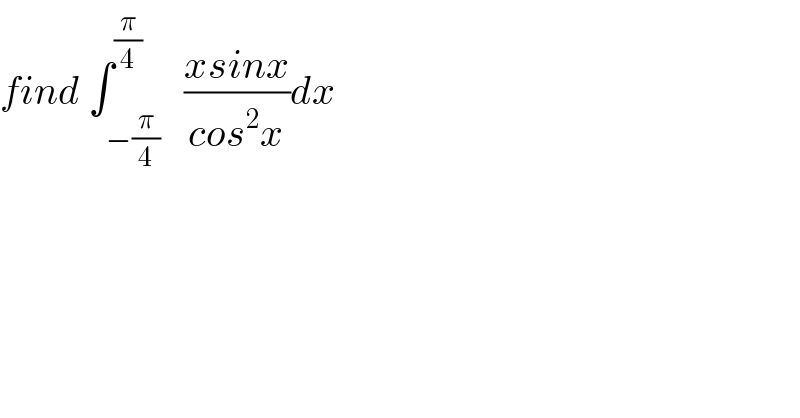
$${find}\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{xsinx}}{{cos}^{\mathrm{2}} {x}}{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
![∫xtanxsecxdx x∫tanxsecxdx−∫[(dx/dx)∫tanxsecxdx]dx xsecx−∫secxdx xsecx−ln(secx+tanx)+c so I=∣xsecx−ln(secx+tanx)∣_((−π)/4) ^(π/4) =[{(π/4)×(√2) −ln((√2) +1)}−{((−π)/4)×(√2) −ln((√2) −1)}] =[2×(π/4)×(√2) +ln((((√2) −1)/( (√2) +1)))] =(π/( (√2)))+ln((((√2) −1)/( (√2) +1)))](https://www.tinkutara.com/question/Q53478.png)
$$\int{xtanxsecxdx} \\ $$$${x}\int{tanxsecxdx}−\int\left[\frac{{dx}}{{dx}}\int{tanxsecxdx}\right]{dx} \\ $$$${xsecx}−\int{secxdx} \\ $$$${xsecx}−{ln}\left({secx}+{tanx}\right)+{c} \\ $$$${so}\:{I}=\mid{xsecx}−{ln}\left({secx}+{tanx}\right)\mid_{\frac{−\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\left[\left\{\frac{\pi}{\mathrm{4}}×\sqrt{\mathrm{2}}\:−{ln}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\right\}−\left\{\frac{−\pi}{\mathrm{4}}×\sqrt{\mathrm{2}}\:−{ln}\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)\right\}\right] \\ $$$$=\left[\mathrm{2}×\frac{\pi}{\mathrm{4}}×\sqrt{\mathrm{2}}\:+{ln}\left(\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}}\right)\right] \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{2}}}+{ln}\left(\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}}\right) \\ $$
