Question Number 53477 by maxmathsup by imad last updated on 22/Jan/19

$${let}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\:\sqrt{{x}+{a}}\:+\mathrm{3}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{also}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\:\sqrt{{x}+{a}}\left(\sqrt{{x}+{a}}\:+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{values}\:{of}\:{integrals}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\:\sqrt{{x}+\mathrm{1}}+\mathrm{3}}\:\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\:\sqrt{{x}+\mathrm{1}}\left(\sqrt{{x}+\mathrm{1}}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Commented by Abdo msup. last updated on 23/Jan/19
![1) we have f(a) =[2((√(x+a))+3)]_0 ^1 =2((√(a+1))−(√a)) 2)we have f^′ (a) =∫_0 ^1 (∂/∂a)( (1/( (√(x+a))+3)))dx =∫_0 ^1 −((((√(x+a))+3)^, )/(((√(x+a))+3)^2 ))dx =−∫_0 ^1 (1/(2((√(x+a)))((√(x+a))+3)^2 ))dx ⇒∫_0 ^1 (dx/(((√(x+a)))((√(x+a))+3)^2 )) =−2f^′ (a) =−4((√(a+1))−(√a))^′ =−4((1/(2(√(a+1)))) −(1/(2(√a)))) =2((1/( (√a))) −(1/( (√(a+1)))))=2(((√(a+1))−(√a))/( (√(a^2 +a)))) 3) we have ∫_0 ^1 (dt/( (√(x+1))+3)) =f(1)=2((√2)−1) ∫_0 ^1 (dx/(((√(x+1)))((√(x+1))+3)^2 )) =−2f^′ (1)=2(((√2)−1)/( (√2))) =(√2)((√2)−1)=2−(√2).](https://www.tinkutara.com/question/Q53575.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\left[\mathrm{2}\left(\sqrt{{x}+{a}}+\mathrm{3}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{2}\left(\sqrt{{a}+\mathrm{1}}−\sqrt{{a}}\right) \\ $$$$\left.\mathrm{2}\right){we}\:{have}\:{f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\partial}{\partial{a}}\left(\:\:\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}+\mathrm{3}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:−\frac{\left(\sqrt{{x}+{a}}+\mathrm{3}\right)^{,} }{\left(\sqrt{{x}+{a}}+\mathrm{3}\right)^{\mathrm{2}} }{dx}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{{x}+{a}}\right)\left(\sqrt{{x}+{a}}+\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\left(\sqrt{{x}+{a}}\right)\left(\sqrt{{x}+{a}}+\mathrm{3}\right)^{\mathrm{2}} }\:=−\mathrm{2}{f}^{'} \left({a}\right) \\ $$$$=−\mathrm{4}\left(\sqrt{{a}+\mathrm{1}}−\sqrt{{a}}\right)^{'} \:=−\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}+\mathrm{1}}}\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}\right) \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\:−\frac{\mathrm{1}}{\:\sqrt{{a}+\mathrm{1}}}\right)=\mathrm{2}\frac{\sqrt{{a}+\mathrm{1}}−\sqrt{{a}}}{\:\sqrt{{a}^{\mathrm{2}} \:+{a}}} \\ $$$$\left.\mathrm{3}\right)\:{we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\:\sqrt{{x}+\mathrm{1}}+\mathrm{3}}\:={f}\left(\mathrm{1}\right)=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\left(\sqrt{{x}+\mathrm{1}}\right)\left(\sqrt{{x}+\mathrm{1}}+\mathrm{3}\right)^{\mathrm{2}} }\:=−\mathrm{2}{f}^{'} \left(\mathrm{1}\right)=\mathrm{2}\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\mathrm{2}−\sqrt{\mathrm{2}}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
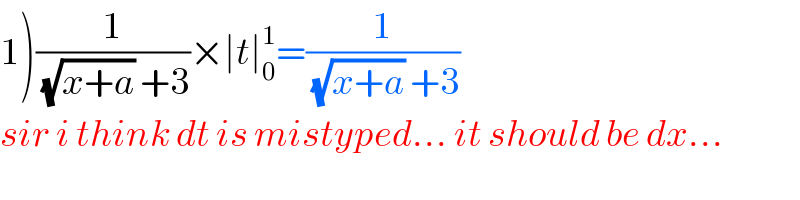
$$\left.\mathrm{1}\right)\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}\:+\mathrm{3}}×\mid{t}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}\:+\mathrm{3}} \\ $$$${sir}\:{i}\:{think}\:{dt}\:{is}\:{mistyped}…\:{it}\:{should}\:{be}\:{dx}… \\ $$
