Question Number 53599 by maxmathsup by imad last updated on 23/Jan/19
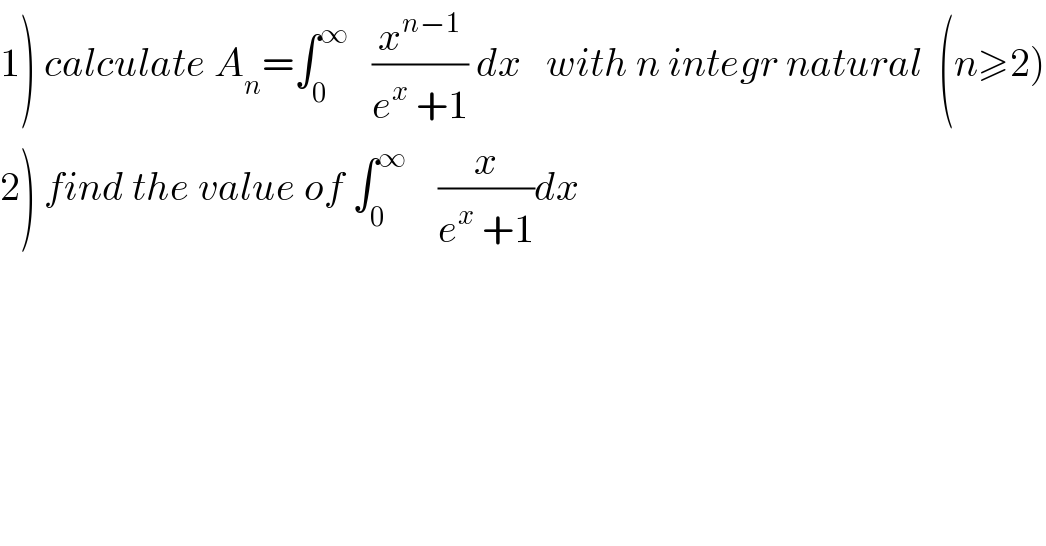
$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{n}−\mathrm{1}} }{{e}^{{x}} \:+\mathrm{1}}\:{dx}\:\:\:{with}\:{n}\:{integr}\:{natural}\:\:\left({n}\geqslant\mathrm{2}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}}{{e}^{{x}} \:+\mathrm{1}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 24/Jan/19
![1) we have A_n =∫_0 ^∞ ((x^(n−1) e^(−x) )/(1+e^(−x) ))dx =∫_0 ^∞ x^(n−1) e^(−x) (Σ_(p=0) ^∞ (−1)^p e^(−px) )dx =Σ_(p=0) ^∞ (−1)^p ∫_0 ^∞ x^(n−1) e^(−(p+1)x) dx =Σ_(p=0) ^∞ (−1)^p A_p A_p =∫_0 ^∞ x^(n−1) e^(−(p+1)x) dx =_((p+1)x=t) ∫_0 ^∞ ((t/(p+1)))^(n−1) e^(−t) (dt/(p+1)) =(1/((p+1)^n )) ∫_0 ^∞ t^(n−1) e^(−t) dt =((Γ(n))/((p+1)^n )) ⇒ A_n =Γ(n) Σ_(p=0) ^∞ (((−1)^p )/((p+1)^n )) =Γ(n).Σ_(p=1) ^∞ (((−1)^(p−1) )/p^n ) let remember ξ(x)=Σ_(p=1) ^∞ (1/p^x ) with x>1 we have Σ_(p=1) ^∞ (((−1)^(p−1) )/p^n ) =−Σ_(k=1) ^∞ (1/((2k)^n )) +Σ_(k=0) ^∞ (1/((2k+1)^n )) =−(1/2^n ) ξ(n) +Σ_(k=0) ^∞ (1/((2k+1)^n )) but ξ(n) =Σ_(p=1) ^∞ (1/p^n ) =Σ_(k=1) ^n (1/((2k)^n )) +Σ_(k=0) ^∞ (1/((2k+1)^n )) =(1/2^n )ξ(n)+Σ_(k=0) ^∞ (1/((2k+1)^n )) ⇒ Σ_(k=0) ^n (1/((2k+1)^n )) =(1−2^(−n) )ξ(n) ⇒Σ_(p=1) ^∞ (((−1)^(p−1) )/p^n ) =−2^(−n) ξ(n) +(1−2^(−n) )ξ(n) =(1−2^(1−n) )ξ(n) ⇒ A_n =(1−2^(1−n) )ξ(n)Γ(n) Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt ⇒Γ(n) =∫_0 ^∞ t^(n−1) e^(−t) dt =[(1/n)t^n e^(−t) ]_0 ^(+∞) +∫_0 ^∞ (t^n /n) e^(−t) dt =(1/n)Γ(n+1) ⇒Γ(n+1)=nΓ(n) ⇒Γ(n+1)=n! ⇒ A_n =(1−2^(1−n) )ξ(n)(n−1)! 2) we see that ∫_0 ^∞ (x/(e^x +1)) dx =A_2 =(1−(1/2))ξ(2) =(1/2).(π^2 /6) =(π^2 /(12)) .](https://www.tinkutara.com/question/Q53655.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{n}−\mathrm{1}} \:{e}^{−{x}} }{\mathrm{1}+{e}^{−{x}} }{dx}\:=\int_{\mathrm{0}} ^{\infty} \:{x}^{{n}−\mathrm{1}} {e}^{−{x}} \left(\sum_{{p}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{p}} {e}^{−{px}} \right){dx} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{p}} \:\int_{\mathrm{0}} ^{\infty} \:{x}^{{n}−\mathrm{1}} \:{e}^{−\left({p}+\mathrm{1}\right){x}} {dx}\:=\sum_{{p}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{p}} \:{A}_{{p}} \\ $$$${A}_{{p}} =\int_{\mathrm{0}} ^{\infty} \:{x}^{{n}−\mathrm{1}} \:{e}^{−\left({p}+\mathrm{1}\right){x}} {dx}\:=_{\left({p}+\mathrm{1}\right){x}={t}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\left(\frac{{t}}{{p}+\mathrm{1}}\right)^{{n}−\mathrm{1}} \:{e}^{−{t}} \:\frac{{dt}}{{p}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\left({p}+\mathrm{1}\right)^{{n}} }\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}−\mathrm{1}} \:{e}^{−{t}} {dt}\:=\frac{\Gamma\left({n}\right)}{\left({p}+\mathrm{1}\right)^{{n}} }\:\Rightarrow\:{A}_{{n}} =\Gamma\left({n}\right)\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}} }{\left({p}+\mathrm{1}\right)^{{n}} } \\ $$$$=\Gamma\left({n}\right).\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}−\mathrm{1}} }{{p}^{{n}} }\:\:\:{let}\:{remember}\:\xi\left({x}\right)=\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{p}^{{x}} }\:\:{with}\:{x}>\mathrm{1} \\ $$$${we}\:{have}\:\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}−\mathrm{1}} }{{p}^{{n}} }\:=−\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{{n}} }\:+\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{{n}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\xi\left({n}\right)\:+\sum_{{k}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{{n}} }\:{but} \\ $$$$\xi\left({n}\right)\:=\sum_{{p}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{p}^{{n}} }\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{{n}} }\:+\sum_{{k}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{{n}} }\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\xi\left({n}\right)+\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{{n}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{{n}} }\:=\left(\mathrm{1}−\mathrm{2}^{−{n}} \right)\xi\left({n}\right)\:\Rightarrow\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}−\mathrm{1}} }{{p}^{{n}} }\:=−\mathrm{2}^{−{n}} \xi\left({n}\right)\:+\left(\mathrm{1}−\mathrm{2}^{−{n}} \right)\xi\left({n}\right) \\ $$$$=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{n}} \right)\xi\left({n}\right)\:\Rightarrow\:{A}_{{n}} =\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{n}} \right)\xi\left({n}\right)\Gamma\left({n}\right) \\ $$$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} \:{dt}\:\Rightarrow\Gamma\left({n}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}−\mathrm{1}} \:{e}^{−{t}} \:{dt}\:=\left[\frac{\mathrm{1}}{{n}}{t}^{{n}} \:{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} +\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\:{e}^{−{t}} {dt} \\ $$$$=\frac{\mathrm{1}}{{n}}\Gamma\left({n}+\mathrm{1}\right)\:\Rightarrow\Gamma\left({n}+\mathrm{1}\right)={n}\Gamma\left({n}\right)\:\Rightarrow\Gamma\left({n}+\mathrm{1}\right)={n}!\:\Rightarrow \\ $$$${A}_{{n}} =\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{n}} \right)\xi\left({n}\right)\left({n}−\mathrm{1}\right)! \\ $$$$\left.\mathrm{2}\right)\:{we}\:{see}\:{that}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}}{{e}^{{x}} +\mathrm{1}}\:{dx}\:={A}_{\mathrm{2}} =\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\xi\left(\mathrm{2}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:. \\ $$
