Question Number 184823 by mnjuly1970 last updated on 12/Jan/23
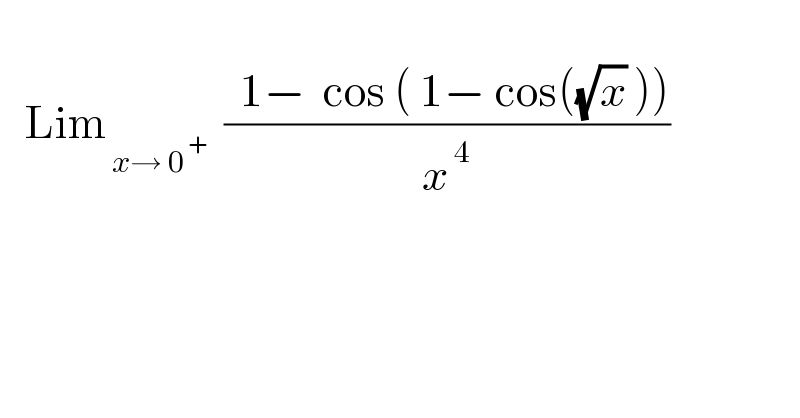
$$ \\ $$$$\:\:\:\mathrm{Lim}_{\:{x}\rightarrow\:\mathrm{0}^{\:+} } \:\:\frac{\:\:\mathrm{1}−\:\:\mathrm{cos}\:\left(\:\mathrm{1}−\:\mathrm{cos}\left(\sqrt{{x}}\:\right)\right)}{{x}^{\:\mathrm{4}} } \\ $$
Answered by cortano1 last updated on 12/Jan/23
![= lim_(x→0^+ ) ((sin^2 (1−cos (√x)))/(2x^4 )) = lim_(x→0^+ ) (((1−cos (√x))^2 [((sin (1−cos (√x)))/(1−cos (√x))) ]^2 )/(2x^4 )) = lim_(x→0^+ ) (((2sin^2 (((√x)/2)))^2 )/(2x^4 )) = 2.lim_(x→0^+ ) (((sin^2 (((√x)/2)))/x^2 ))^2 =2.lim_(x→0^+ ) ((1/(4x)))^2 = ∞](https://www.tinkutara.com/question/Q184825.png)
$$=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\sqrt{{x}}\right)}{\mathrm{2}{x}^{\mathrm{4}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\mathrm{cos}\:\sqrt{{x}}\right)^{\mathrm{2}} \:\left[\frac{\mathrm{sin}\:\left(\mathrm{1}−\mathrm{cos}\:\sqrt{{x}}\right)}{\mathrm{1}−\mathrm{cos}\:\sqrt{{x}}}\:\right]^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{4}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\left(\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\sqrt{{x}}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{4}} } \\ $$$$=\:\mathrm{2}.\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\sqrt{{x}}}{\mathrm{2}}\right)}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}.\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{4}{x}}\right)^{\mathrm{2}} =\:\infty \\ $$
