Question Number 185085 by Ml last updated on 16/Jan/23

$$\mathrm{log}_{\mathrm{3}} \left(\mathrm{a}+\mathrm{1}\right)=\mathrm{log}_{\mathrm{4}} \left(\mathrm{a}+\mathrm{8}\right) \\ $$$$\mathrm{a}=?? \\ $$$$\mathrm{please}\:\mathrm{solution} \\ $$
Answered by Frix last updated on 16/Jan/23
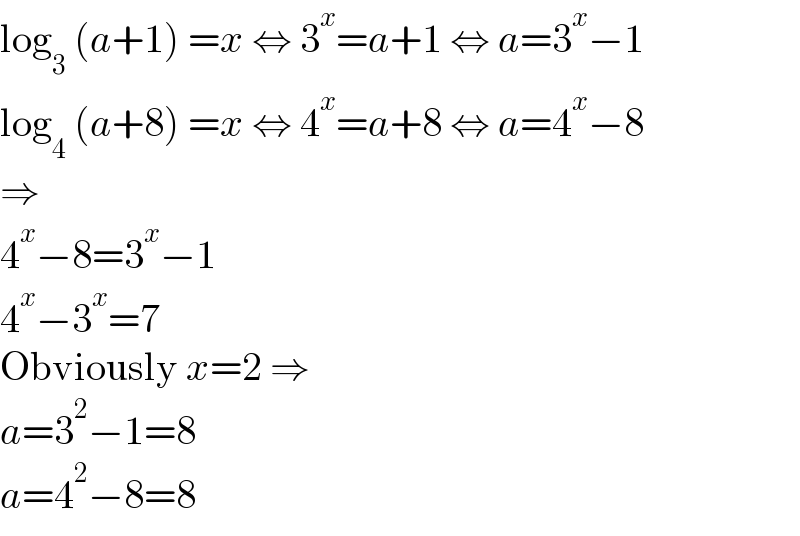
$$\mathrm{log}_{\mathrm{3}} \:\left({a}+\mathrm{1}\right)\:={x}\:\Leftrightarrow\:\mathrm{3}^{{x}} ={a}+\mathrm{1}\:\Leftrightarrow\:{a}=\mathrm{3}^{{x}} −\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{4}} \:\left({a}+\mathrm{8}\right)\:={x}\:\Leftrightarrow\:\mathrm{4}^{{x}} ={a}+\mathrm{8}\:\Leftrightarrow\:{a}=\mathrm{4}^{{x}} −\mathrm{8} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}^{{x}} −\mathrm{8}=\mathrm{3}^{{x}} −\mathrm{1} \\ $$$$\mathrm{4}^{{x}} −\mathrm{3}^{{x}} =\mathrm{7} \\ $$$$\mathrm{Obviously}\:{x}=\mathrm{2}\:\Rightarrow \\ $$$${a}=\mathrm{3}^{\mathrm{2}} −\mathrm{1}=\mathrm{8} \\ $$$${a}=\mathrm{4}^{\mathrm{2}} −\mathrm{8}=\mathrm{8} \\ $$
Answered by aba last updated on 16/Jan/23
![consider the function f(x)=log_3 (x+1)−log_4 (x+8) Df=]−1,+∞[ f^′ (x)=(1/((x+1)ln(3)))−(1/((x+8)ln(4))) =(((x+8)ln(4)−(x+1)ln(3))/((x+1)(x+8)ln(3)ln(4))) =((x(ln(4)−ln(3))+8ln(4)−ln(3))/((x+1)(x+8)ln(3)ln(4))) the denominator is positive on the domain of f f′(x)=0 ⇒ x(ln(4)−ln(3))+8ln(4)−ln(3)=0 ⇒ x=−((8ln(4)−ln(3))/(ln(4)−ln(3))) ⇒x=−((ln((4^8 /3)))/(ln((4/3)))) <−1 ⇒x<−1 so the function f is strictly increasing on ]−1,+∞[. Hence the equation f(x)=0 has at most one solution since f(8)=0, we found it](https://www.tinkutara.com/question/Q185092.png)
$$\mathrm{consider}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{log}_{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)−\mathrm{log}_{\mathrm{4}} \left(\mathrm{x}+\mathrm{8}\right) \\ $$$$\left.\:\:\:\mathrm{Df}=\right]−\mathrm{1},+\infty\left[\right. \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{ln}\left(\mathrm{3}\right)}−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{8}\right)\mathrm{ln}\left(\mathrm{4}\right)} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{x}+\mathrm{8}\right)\mathrm{ln}\left(\mathrm{4}\right)−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{ln}\left(\mathrm{3}\right)}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{8}\right)\mathrm{ln}\left(\mathrm{3}\right)\mathrm{ln}\left(\mathrm{4}\right)} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{x}\left(\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{3}\right)\right)+\mathrm{8ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{3}\right)}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{8}\right)\mathrm{ln}\left(\mathrm{3}\right)\mathrm{ln}\left(\mathrm{4}\right)} \\ $$$$\mathrm{the}\:\mathrm{denominator}\:\mathrm{is}\:\mathrm{positive}\:\mathrm{on}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{f} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow\:\mathrm{x}\left(\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{3}\right)\right)+\mathrm{8ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{x}=−\frac{\mathrm{8ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{3}\right)}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{3}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}=−\frac{\mathrm{ln}\left(\frac{\mathrm{4}^{\mathrm{8}} }{\mathrm{3}}\right)}{\mathrm{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)}\:<−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}<−\mathrm{1} \\ $$$$\left.\mathrm{so}\:\mathrm{the}\:\mathrm{function}\:\mathrm{f}\:\mathrm{is}\:\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{on}\:\right]−\mathrm{1},+\infty\left[.\:\mathrm{Hence}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\mathrm{has}\:\mathrm{at}\:\mathrm{most}\:\mathrm{one}\:\mathrm{solution}\right. \\ $$$$\mathrm{since}\:\mathrm{f}\left(\mathrm{8}\right)=\mathrm{0},\:\mathrm{we}\:\mathrm{found}\:\mathrm{it} \\ $$
