Question Number 185983 by mnjuly1970 last updated on 30/Jan/23
![{ (( f : [ 0 , 1 ] → R)),(( f (x ) = (( 4^( x) )/(2 + 4^( x) )))) :} is given . find the value of the following expression. E = f ((1/(20)) )+ f((( 2)/(20)) )+... +f (((19)/(20))) −f ((1/2) )=?](https://www.tinkutara.com/question/Q185983.png)
$$ \\ $$$$\:\:\:\:\:\begin{cases}{\:\:\:{f}\::\:\:\left[\:\:\mathrm{0}\:\:,\:\:\mathrm{1}\:\right]\:\rightarrow\:\mathbb{R}}\\{\:\:\:\:{f}\:\left({x}\:\right)\:=\:\frac{\:\mathrm{4}^{\:{x}} }{\mathrm{2}\:+\:\mathrm{4}^{\:{x}} }}\end{cases} \\ $$$$\:\:\:\:\:\:{is}\:\:{given}\:.\:\:{find}\:{the}\:{value}\:{of} \\ $$$$\:\:\:\:\:\:{the}\:{following}\:{expression}. \\ $$$$\:\:\:\:\:\:\mathrm{E}\:=\:{f}\:\left(\frac{\mathrm{1}}{\mathrm{20}}\:\right)+\:{f}\left(\frac{\:\mathrm{2}}{\mathrm{20}}\:\right)+…\:+{f}\:\left(\frac{\mathrm{19}}{\mathrm{20}}\right)\:−{f}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:\right)=? \\ $$
Answered by ARUNG_Brandon_MBU last updated on 30/Jan/23
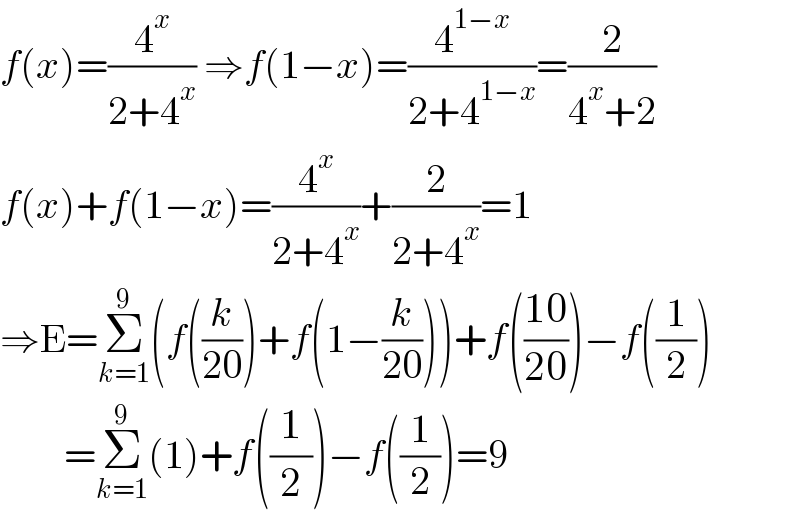
$${f}\left({x}\right)=\frac{\mathrm{4}^{{x}} }{\mathrm{2}+\mathrm{4}^{{x}} }\:\Rightarrow{f}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{4}^{\mathrm{1}−{x}} }{\mathrm{2}+\mathrm{4}^{\mathrm{1}−{x}} }=\frac{\mathrm{2}}{\mathrm{4}^{{x}} +\mathrm{2}} \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{4}^{{x}} }{\mathrm{2}+\mathrm{4}^{{x}} }+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{4}^{{x}} }=\mathrm{1} \\ $$$$\Rightarrow\mathrm{E}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left({f}\left(\frac{{k}}{\mathrm{20}}\right)+{f}\left(\mathrm{1}−\frac{{k}}{\mathrm{20}}\right)\right)+{f}\left(\frac{\mathrm{10}}{\mathrm{20}}\right)−{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left(\mathrm{1}\right)+{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{9} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 30/Jan/23
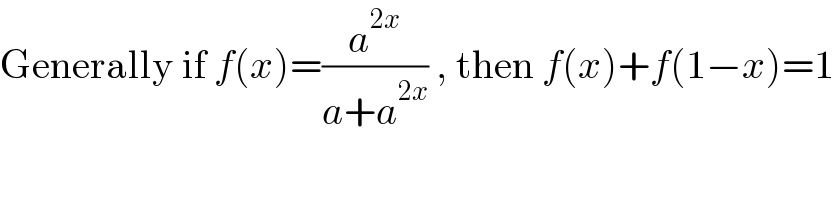
$$\mathrm{Generally}\:\mathrm{if}\:{f}\left({x}\right)=\frac{{a}^{\mathrm{2}{x}} }{{a}+{a}^{\mathrm{2}{x}} }\:,\:\mathrm{then}\:{f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)=\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 30/Jan/23

$${thanks}\:{alot}\:{sir}\:{Arung} \\ $$
