Question Number 55280 by Abdo msup. last updated on 20/Feb/19
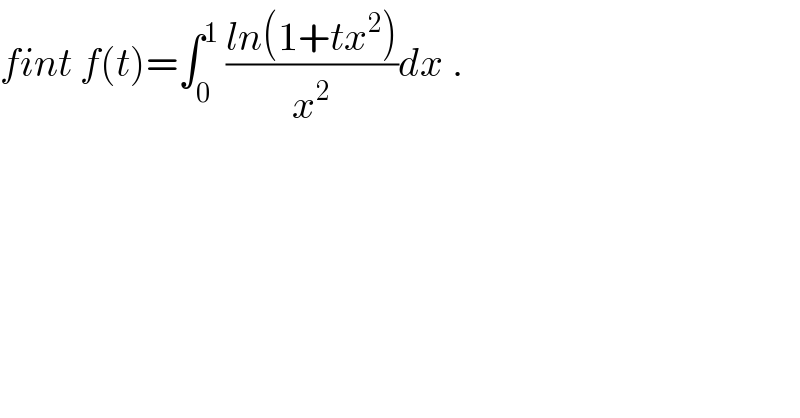
$${fint}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 20/Feb/19
![we have f^′ (t) =∫_0 ^1 (∂/∂t)(((ln(1+tx^2 ))/x^2 ))dx =∫_0 ^1 (1/x^2 ) (x^2 /(1+tx^2 ))dx = ∫_0 ^1 (dx/(1+tx^2 )) so if t≥0 we get f^′ (t)=_((√t)x =u) ∫_0 ^(√t) (du/( (√t)(1+u^2 ))) =(1/( (√t)))[arctan(u)]_0 ^(√t) =((arctan((√t)))/( (√t))) ⇒f(t) =∫_0 ^t ((arctan((√u)))/( (√u))) du +λ λ=f(0)=0 ⇒f(t) =∫_0 ^t ((arctan((√u)))/( (√u))) du =_((√u)=x) ∫_0 ^(√t) ((arctanx)/x) (2x)dx =2 ∫_0 ^(√t) arctanx dx by parts f(t)=2{ [xarctanx]_0 ^(√t) −∫_0 ^(√t) (x/(1+x^2 ))dx} =2{(√t)arctan((√t)) −[(1/2)ln(1+x^2 )]_0 ^(√t) ⇒f(t)=2(√t)arctan((√t))−ln(1+t) . it t<0 we get f^′ (t) =∫_0 ^1 (dx/(1−(−t)x^2 )) =∫_0 ^1 (dx/((1−(√(−t))x)(1+(√(−t))x))) =(1/2)∫_0 ^1 ( (1/(1−(√(−t))x)) +(1/(1+(√(−t))x)))dx =(1/(2(√(−t)))) { ∫_0 ^1 ((√(−t))/(1−(√(−t))x)) +∫_0 ^1 ((√(−t))/(1+(√(−t))x))dx} =(1/(2(√(−t))))[ln∣1+(√(−t))x∣−ln∣1−(√(−t))x∣]_(x=0) ^(x=1) =(1/(2(√(−t)))) ln∣((1+(√(−t)))/(1−(√(−t))))∣ ⇒ f(t) =∫(1/(2(√(−t))))ln∣((1+(√(−t)))/(1−(√(−t))))∣dt +c =_((√(−t))=x) ∫ (1/(2x))ln∣((1+x)/(1−x))∣(−2x)dx +c = c−∫ ln∣1+x∣dx+∫ln∣1−x∣dx](https://www.tinkutara.com/question/Q55299.png)
$${we}\:{have}\:{f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\partial}{\partial{t}}\left(\frac{{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\right){dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{tx}^{\mathrm{2}} }{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+{tx}^{\mathrm{2}} }\:\:\:{so}\:\:{if}\:{t}\geqslant\mathrm{0}\:\:{we}\:{get}\:{f}^{'} \left({t}\right)=_{\sqrt{{t}}{x}\:={u}} \:\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \:\:\:\:\frac{{du}}{\:\sqrt{{t}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{t}}}\left[{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{\sqrt{{t}}} \:=\frac{{arctan}\left(\sqrt{{t}}\right)}{\:\sqrt{{t}}}\:\Rightarrow{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{{t}} \:\:\frac{{arctan}\left(\sqrt{{u}}\right)}{\:\sqrt{{u}}}\:{du}\:+\lambda \\ $$$$\lambda={f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{{t}} \:\:\frac{{arctan}\left(\sqrt{{u}}\right)}{\:\sqrt{{u}}}\:{du}\:=_{\sqrt{{u}}={x}} \:\:\:\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \:\frac{{arctanx}}{{x}}\:\left(\mathrm{2}{x}\right){dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{{t}}} {arctanx}\:{dx}\:\:{by}\:{parts}\:{f}\left({t}\right)=\mathrm{2}\left\{\:\left[{xarctanx}\right]_{\mathrm{0}} ^{\sqrt{{t}}} \:−\int_{\mathrm{0}} ^{\sqrt{{t}}} \:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right\} \\ $$$$=\mathrm{2}\left\{\sqrt{{t}}{arctan}\left(\sqrt{{t}}\right)\:−\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\sqrt{{t}}} \Rightarrow{f}\left({t}\right)=\mathrm{2}\sqrt{{t}}{arctan}\left(\sqrt{{t}}\right)−{ln}\left(\mathrm{1}+{t}\right)\:.\right. \\ $$$${it}\:{t}<\mathrm{0}\:\:{we}\:{get}\:{f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{1}−\left(−{t}\right){x}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\left(\mathrm{1}−\sqrt{−{t}}{x}\right)\left(\mathrm{1}+\sqrt{−{t}}{x}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:\frac{\mathrm{1}}{\mathrm{1}−\sqrt{−{t}}{x}}\:+\frac{\mathrm{1}}{\mathrm{1}+\sqrt{−{t}}{x}}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{t}}}\:\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{−{t}}}{\mathrm{1}−\sqrt{−{t}}{x}}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{−{t}}}{\mathrm{1}+\sqrt{−{t}}{x}}{dx}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{t}}}\left[{ln}\mid\mathrm{1}+\sqrt{−{t}}{x}\mid−{ln}\mid\mathrm{1}−\sqrt{−{t}}{x}\mid\right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{t}}}\:{ln}\mid\frac{\mathrm{1}+\sqrt{−{t}}}{\mathrm{1}−\sqrt{−{t}}}\mid\:\Rightarrow\:{f}\left({t}\right)\:=\int\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{t}}}{ln}\mid\frac{\mathrm{1}+\sqrt{−{t}}}{\mathrm{1}−\sqrt{−{t}}}\mid{dt}\:+{c} \\ $$$$=_{\sqrt{−{t}}={x}} \:\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{2}{x}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\left(−\mathrm{2}{x}\right){dx}\:+{c}\:=\:{c}−\int\:{ln}\mid\mathrm{1}+{x}\mid{dx}+\int{ln}\mid\mathrm{1}−{x}\mid{dx}\: \\ $$
Answered by tm888 last updated on 20/Feb/19

