Question Number 56339 by Tinkutara last updated on 14/Mar/19
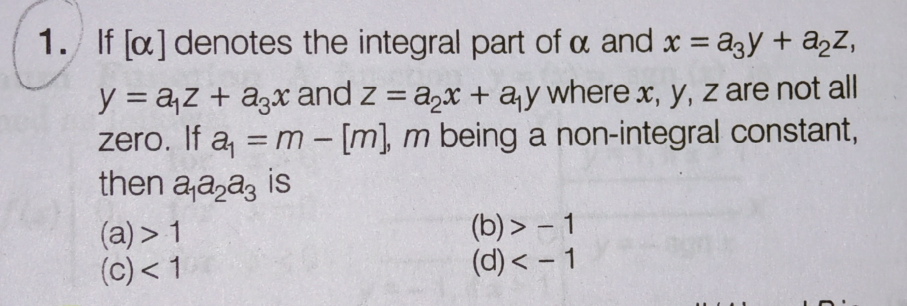
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Mar/19
![x=a_3 y+a_2 (a_2 x+a_1 y) x−a_2 ^2 x=y(a_3 +a_1 a_2 ) x(1−a_2 ^2 )=y(a_3 +a_1 a_2 ) (x/y)=((a_3 +a_1 a_2 )/(1−a_2 ^2 )) y=a_1 (a_2 x+a_1 y)+a_3 x y(1−a_1 ^2 )=x(a_3 +a_1 a_2 ) (x/y)=((1−a_1 ^2 )/(a_3 +a_1 a_2 )) hence ((a_3 +a_1 a_2 )/(1−a_2 ^2 ))=((1−a_1 ^2 )/(a_3 +a_1 a_2 )) a_3 ^2 +2a_1 a_2 a_3 +a_1 ^2 a_2 ^2 =1−a_1 ^2 −a_2 ^2 +a_1 ^2 a_2 ^2 a_1 a_2 a_3 =(1/2){1−(a_1 ^2 +a_2 ^2 +a_3 ^2 )} 1)a_1 =m−[m]={m}←fractional part so 1 >a_1 ^2 >0 but no mention of a_2 and a_3 in question so conclusion can not be drawn... let other check...](https://www.tinkutara.com/question/Q56353.png)
$${x}={a}_{\mathrm{3}} {y}+{a}_{\mathrm{2}} \left({a}_{\mathrm{2}} {x}+{a}_{\mathrm{1}} {y}\right) \\ $$$${x}−{a}_{\mathrm{2}} ^{\mathrm{2}} {x}={y}\left({a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} \right) \\ $$$${x}\left(\mathrm{1}−{a}_{\mathrm{2}} ^{\mathrm{2}} \right)={y}\left({a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} \right) \\ $$$$\frac{{x}}{{y}}=\frac{{a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} }{\mathrm{1}−{a}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$${y}={a}_{\mathrm{1}} \left({a}_{\mathrm{2}} {x}+{a}_{\mathrm{1}} {y}\right)+{a}_{\mathrm{3}} {x} \\ $$$${y}\left(\mathrm{1}−{a}_{\mathrm{1}} ^{\mathrm{2}} \right)={x}\left({a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} \right) \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{1}−{a}_{\mathrm{1}} ^{\mathrm{2}} }{{a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} } \\ $$$${hence} \\ $$$$\frac{{a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} }{\mathrm{1}−{a}_{\mathrm{2}} ^{\mathrm{2}} }=\frac{\mathrm{1}−{a}_{\mathrm{1}} ^{\mathrm{2}} }{{a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} } \\ $$$${a}_{\mathrm{3}} ^{\mathrm{2}} +\mathrm{2}{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} +{a}_{\mathrm{1}} ^{\mathrm{2}} {a}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{1}−{a}_{\mathrm{1}} ^{\mathrm{2}} −{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{1}} ^{\mathrm{2}} {a}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}−\left({a}_{\mathrm{1}} ^{\mathrm{2}} +{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} \right)\right\} \\ $$$$\left.\mathrm{1}\right){a}_{\mathrm{1}} ={m}−\left[{m}\right]=\left\{{m}\right\}\leftarrow{fractional}\:{part} \\ $$$${so}\:\:\:\:\:\:\:\mathrm{1}\:>{a}_{\mathrm{1}} ^{\mathrm{2}} >\mathrm{0} \\ $$$$\boldsymbol{{but}}\:\boldsymbol{{no}}\:\boldsymbol{{mention}}\:\boldsymbol{{of}}\:\boldsymbol{{a}}_{\mathrm{2}} \:\boldsymbol{{and}}\:\boldsymbol{{a}}_{\mathrm{3}} \:\boldsymbol{{in}}\:\boldsymbol{{question}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{conclusion}}\:\boldsymbol{{can}}\:\boldsymbol{{not}}\:\boldsymbol{{be}}\:\boldsymbol{{drawn}}… \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{other}}\:\boldsymbol{{check}}… \\ $$$$ \\ $$$$ \\ $$
