Question Number 121965 by bemath last updated on 13/Nov/20
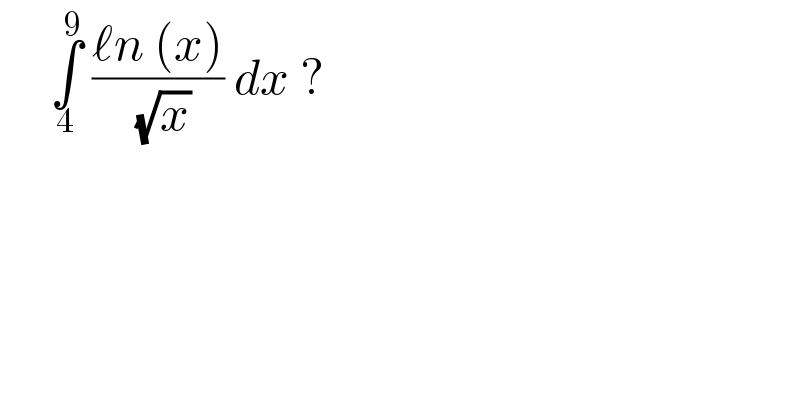
$$\:\:\:\:\:\underset{\mathrm{4}} {\overset{\mathrm{9}} {\int}}\:\frac{\ell{n}\:\left({x}\right)}{\:\sqrt{{x}}}\:{dx}\:? \\ $$
Answered by bemath last updated on 13/Nov/20
![∫_4 ^9 ((ℓn(x))/( (√x))) dx = ∫_2 ^3 ((ℓn(u^2 ))/u)(2u du) = ∫_2 ^3 4ℓn(u) du = 4 ( u ℓn (u)−u ) ]_2 ^3 = 4{(3(ℓn(3)−1)−(2(ℓn(2)−1)} = 4(ℓn(((27)/4))−1)](https://www.tinkutara.com/question/Q121967.png)
$$\:\underset{\mathrm{4}} {\overset{\mathrm{9}} {\int}}\:\frac{\ell{n}\left({x}\right)}{\:\sqrt{{x}}}\:{dx}\:=\:\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}\:\frac{\ell{n}\left({u}^{\mathrm{2}} \right)}{{u}}\left(\mathrm{2}{u}\:{du}\right) \\ $$$$=\:\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}\:\mathrm{4}\ell{n}\left({u}\right)\:{du}\: \\ $$$$\left.=\:\mathrm{4}\:\left(\:{u}\:\ell{n}\:\left({u}\right)−{u}\:\right)\:\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\:\mathrm{4}\left\{\left(\mathrm{3}\left(\ell{n}\left(\mathrm{3}\right)−\mathrm{1}\right)−\left(\mathrm{2}\left(\ell{n}\left(\mathrm{2}\right)−\mathrm{1}\right)\right\}\right.\right. \\ $$$$=\:\mathrm{4}\left(\ell{n}\left(\frac{\mathrm{27}}{\mathrm{4}}\right)−\mathrm{1}\right) \\ $$
Answered by Bird last updated on 13/Nov/20
![∫_4 ^(9 ) ((lnx)/( (√x)))dx =_((√x)=t) ∫_2 ^(3 ) ((2lnt)/t)(2tdt) =4∫_2 ^3 lnt dt =4[tlnt −t]_2 ^3 =4{3ln3−3−2ln2+2} =4{3ln(3)−2ln2−1}](https://www.tinkutara.com/question/Q122018.png)
$$\int_{\mathrm{4}} ^{\mathrm{9}\:} \:\frac{{lnx}}{\:\sqrt{{x}}}{dx}\:=_{\sqrt{{x}}={t}} \:\:\:\:\int_{\mathrm{2}} ^{\mathrm{3}\:} \:\frac{\mathrm{2}{lnt}}{{t}}\left(\mathrm{2}{tdt}\right) \\ $$$$=\mathrm{4}\int_{\mathrm{2}} ^{\mathrm{3}} {lnt}\:{dt}\:\:=\mathrm{4}\left[{tlnt}\:−{t}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\mathrm{4}\left\{\mathrm{3}{ln}\mathrm{3}−\mathrm{3}−\mathrm{2}{ln}\mathrm{2}+\mathrm{2}\right\} \\ $$$$=\mathrm{4}\left\{\mathrm{3}{ln}\left(\mathrm{3}\right)−\mathrm{2}{ln}\mathrm{2}−\mathrm{1}\right\} \\ $$
