Question Number 57124 by necx1 last updated on 30/Mar/19
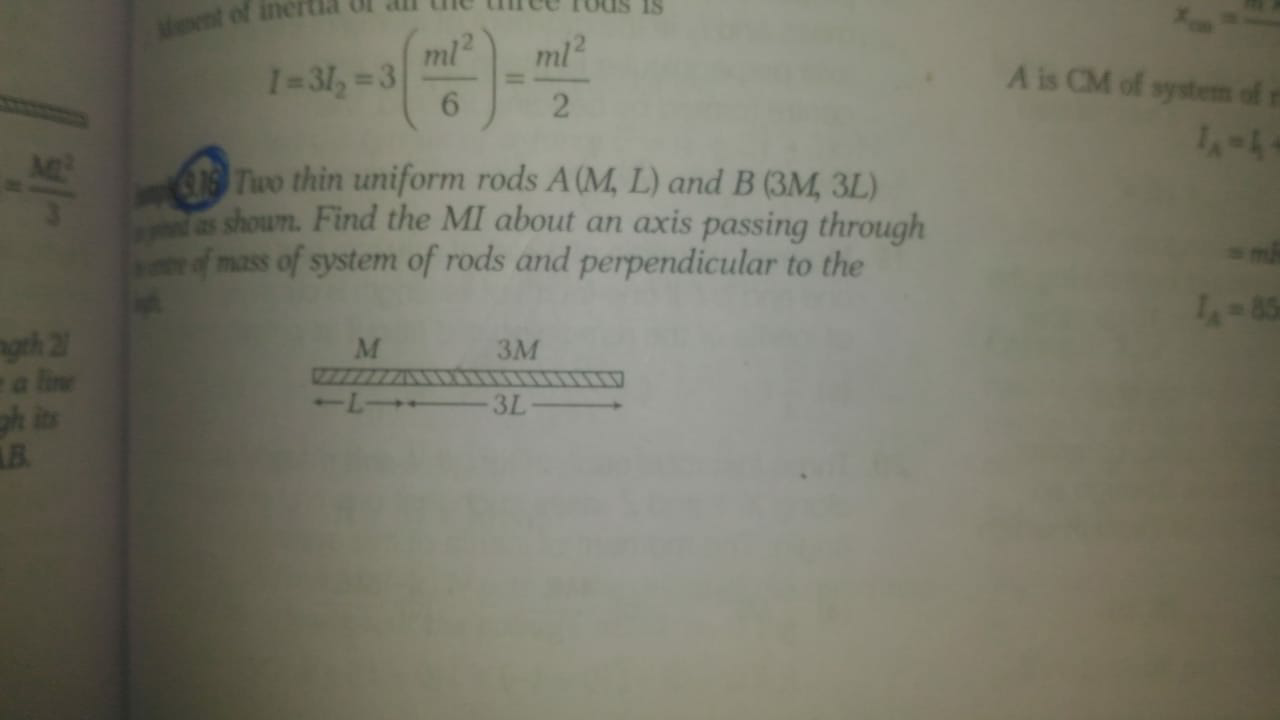
Commented by necx1 last updated on 30/Mar/19

$${please}\:{help} \\ $$
Commented by mr W last updated on 31/Mar/19
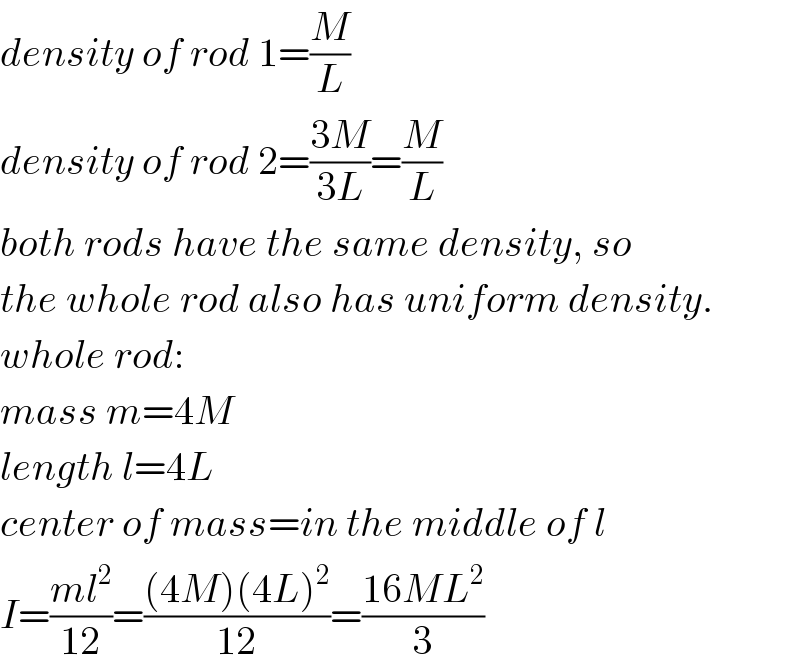
$${density}\:{of}\:{rod}\:\mathrm{1}=\frac{{M}}{{L}} \\ $$$${density}\:{of}\:{rod}\:\mathrm{2}=\frac{\mathrm{3}{M}}{\mathrm{3}{L}}=\frac{{M}}{{L}} \\ $$$${both}\:{rods}\:{have}\:{the}\:{same}\:{density},\:{so} \\ $$$${the}\:{whole}\:{rod}\:{also}\:{has}\:{uniform}\:{density}. \\ $$$${whole}\:{rod}: \\ $$$${mass}\:{m}=\mathrm{4}{M} \\ $$$${length}\:{l}=\mathrm{4}{L} \\ $$$${center}\:{of}\:{mass}={in}\:{the}\:{middle}\:{of}\:{l} \\ $$$${I}=\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}=\frac{\left(\mathrm{4}{M}\right)\left(\mathrm{4}{L}\right)^{\mathrm{2}} }{\mathrm{12}}=\frac{\mathrm{16}{ML}^{\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by necx1 last updated on 31/Mar/19
$${hmmm}….{This}\:{is}\:{really}\:{simple}\:{to}\:{understand}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 31/Mar/19
![1)[origin (0,0,0) is taken at free end of rod L] 2)co ordinate of joined end of two rod(L,0,0) 3)co ordinate of free end of rod 3L(4L,0,0) 4)co ordinate of centre of mass of rod of lengthL ((L/2),0,0) 5)co ordinate of C.M of rod of length 3L {(L+((3L)/(2 ))),0,0}=(((5L)/2),0,0) co ordinate of centre of mass combined rod is x=((m×(L/2)+3m×((5L)/2))/(m+3m))=((8mL)/(4m))=2L c.m(2L,0,0) Moment of inertia =M×(L^2 /(12))+M(2L−(L/2))^2 +3M×(((3L)^2 )/(12))+3M(2L−((5L)/2))^2 =((ML^2 )/(12))+((M×9L^2 )/4)+((3M×9L^2 )/(12))+((3M×L^2 )/4) =((28ML^2 )/(12))+((12ML^2 )/4) =((28ML^2 +36ML^2 )/(12))=((64ML^2 )/(12))=((16ML^2 )/3) pls check is it correct](https://www.tinkutara.com/question/Q57158.png)
$$ \\ $$$$\left.\mathrm{1}\right)\left[{origin}\:\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:{is}\:{taken}\:{at}\:{free}\:{end}\:{of}\:{rod}\:{L}\right] \\ $$$$\left.\mathrm{2}\right){co}\:{ordinate}\:{of}\:{joined}\:{end}\:{of}\:{two}\:{rod}\left({L},\mathrm{0},\mathrm{0}\right) \\ $$$$\left.\mathrm{3}\right){co}\:{ordinate}\:{of}\:{free}\:{end}\:{of}\:{rod}\:\mathrm{3}{L}\left(\mathrm{4}{L},\mathrm{0},\mathrm{0}\right) \\ $$$$\left.\mathrm{4}\right){co}\:{ordinate}\:{of}\:{centre}\:{of}\:{mass}\:{of}\:{rod}\:{of}\:{lengthL} \\ $$$$\left(\frac{{L}}{\mathrm{2}},\mathrm{0},\mathrm{0}\right) \\ $$$$\left.\mathrm{5}\right){co}\:{ordinate}\:{of}\:{C}.{M}\:{of}\:{rod}\:{of}\:{length}\:\mathrm{3}{L} \\ $$$$\:\left\{\left({L}+\frac{\mathrm{3}{L}}{\mathrm{2}\:}\right),\mathrm{0},\mathrm{0}\right\}=\left(\frac{\mathrm{5}{L}}{\mathrm{2}},\mathrm{0},\mathrm{0}\right) \\ $$$${co}\:{ordinate}\:{of}\:\boldsymbol{{centre}}\:\boldsymbol{{of}}\:\boldsymbol{{mass}}\:\boldsymbol{{combined}}\:\boldsymbol{{rod}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{x}}=\frac{\boldsymbol{{m}}×\frac{\boldsymbol{{L}}}{\mathrm{2}}+\mathrm{3}{m}×\frac{\mathrm{5}{L}}{\mathrm{2}}}{{m}+\mathrm{3}{m}}=\frac{\mathrm{8}{mL}}{\mathrm{4}{m}}=\mathrm{2}{L} \\ $$$${c}.{m}\left(\mathrm{2}{L},\mathrm{0},\mathrm{0}\right) \\ $$$${Moment}\:{of}\:{inertia} \\ $$$$={M}×\frac{{L}^{\mathrm{2}} }{\mathrm{12}}+{M}\left(\mathrm{2}{L}−\frac{{L}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{3}{M}×\frac{\left(\mathrm{3}{L}\right)^{\mathrm{2}} }{\mathrm{12}}+\mathrm{3}{M}\left(\mathrm{2}{L}−\frac{\mathrm{5}{L}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\frac{{ML}^{\mathrm{2}} }{\mathrm{12}}+\frac{{M}×\mathrm{9}{L}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{3}{M}×\mathrm{9}{L}^{\mathrm{2}} }{\mathrm{12}}+\frac{\mathrm{3}{M}×{L}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\mathrm{28}{ML}^{\mathrm{2}} }{\mathrm{12}}+\frac{\mathrm{12}{ML}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\mathrm{28}{ML}^{\mathrm{2}} +\mathrm{36}{ML}^{\mathrm{2}} }{\mathrm{12}}=\frac{\mathrm{64}{ML}^{\mathrm{2}} }{\mathrm{12}}=\frac{\mathrm{16}{ML}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${pls}\:{check}\:{is}\:{it}\:{correct} \\ $$
Commented by necx1 last updated on 31/Mar/19
$${indepth}\:{sir}….{Thank}\:{you}\:{for}\:{your}\:{help}. \\ $$$${I}'{ve}\:{learnt}\:{so}\:{much}\:{sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 31/Mar/19
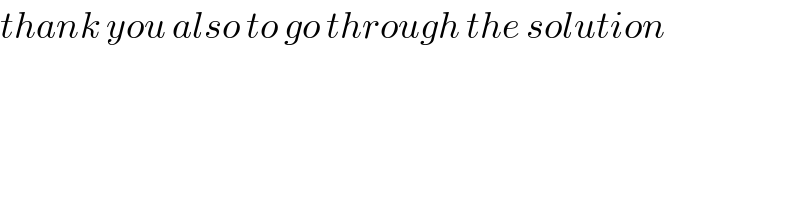
$${thank}\:{you}\:{also}\:{to}\:{go}\:{through}\:{the}\:{solution} \\ $$
