Question Number 57325 by turbo msup by abdo last updated on 02/Apr/19
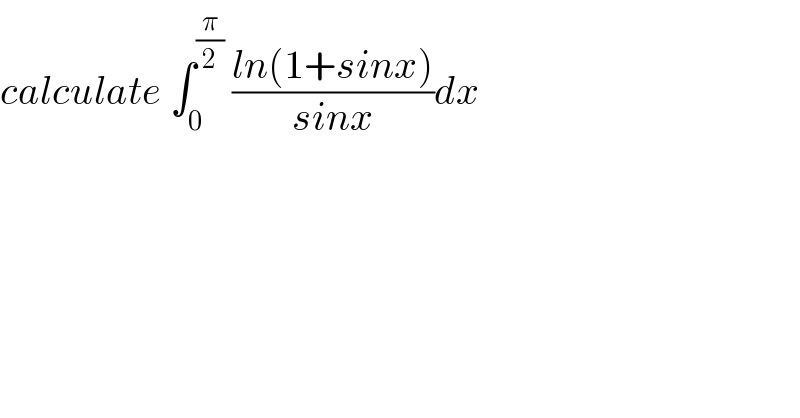
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{ln}\left(\mathrm{1}+{sinx}\right)}{{sinx}}{dx} \\ $$
Commented by Abdo msup. last updated on 05/Apr/19
![let f(t) =∫_0 ^(π/2) ((ln(1+t sinx))/(sinx))dx with 0≤t≤1 we have f^′ (t) =∫_0 ^(π/2) ((sinx)/(sinx(1+tsinx)))dx =∫_0 ^(π/2) (dx/(1+tsinx)) =_(tan((x/2))=u) ∫_0 ^1 ((2du)/((1+u^2 )(1+t ((2u)/(1+u^2 ))))) =∫_0 ^1 ((2du)/(1+u^2 +2tu)) =∫_0 ^1 ((2du)/(u^2 +2tu +1)) =∫_0 ^1 ((2du)/(u^2 +2tu +u^2 +1−u^2 )) =∫_0 ^1 ((2du)/((u+t)^2 +1−t^2 )) =_(u+t =(√(1−t^2 ))α) ∫_(t/( (√(1−t2)))) ^((1+t)/( (√(1−t^2 )))) ((2(√(1−t^2 ))dα)/((1−t^2 )(1+α^2 ))) =(2/( (√(1−t^2 )))) [ arctan(α)]_(t/( (√(1−t^2 )))) ^((1+t)/( (√(1−t^2 )))) =(2/( (√(1−t^2 )))){ arctan(((1+t)/( (√(1−t^2 )))))−arctan((t/( (√(1−t^2 )))))} ⇒ f(t) = ∫ (2/( (√(1−t^2 )))) arctan(((1+t)/( (√(1−t^2 )))))dt −∫ (2/( (√(1−t^2 )))) arctan((t/( (√(1−t^2 )))))dt +c ....be continued..=](https://www.tinkutara.com/question/Q57482.png)
$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{ln}\left(\mathrm{1}+{t}\:{sinx}\right)}{{sinx}}{dx}\:\:{with}\:\mathrm{0}\leqslant{t}\leqslant\mathrm{1} \\ $$$${we}\:{have}\:{f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sinx}}{{sinx}\left(\mathrm{1}+{tsinx}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\mathrm{1}+{tsinx}}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={u}} \:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{tu}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}{tu}\:+\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}{tu}\:+{u}^{\mathrm{2}} \:+\mathrm{1}−{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{du}}{\left({u}+{t}\right)^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$=_{{u}+{t}\:=\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\alpha} \:\:\:\:\:\int_{\frac{{t}}{\:\sqrt{\mathrm{1}−{t}\mathrm{2}}}} ^{\frac{\mathrm{1}+{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}} \:\:\:\:\frac{\mathrm{2}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{d}\alpha}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\left[\:{arctan}\left(\alpha\right)\right]_{\frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}} ^{\frac{\mathrm{1}+{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\left\{\:{arctan}\left(\frac{\mathrm{1}+{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right)−{arctan}\left(\frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right)\right\}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\:\int\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{1}+{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt} \\ $$$$−\int\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:{arctan}\left(\frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt}\:+{c}\:….{be}\:{continued}..= \\ $$
