Question Number 123687 by mnjuly1970 last updated on 27/Nov/20
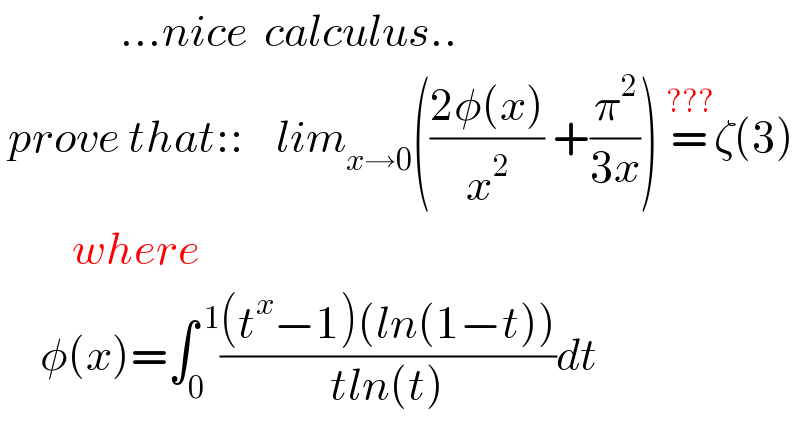
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{calculus}.. \\ $$$$\:{prove}\:{that}::\:\:\:\:{lim}_{{x}\rightarrow\mathrm{0}} \left(\frac{\mathrm{2}\phi\left({x}\right)}{{x}^{\mathrm{2}} }\:+\frac{\pi^{\mathrm{2}} }{\mathrm{3}{x}}\right)\:\overset{???} {=}\zeta\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{where} \\ $$$$\:\:\:\:\:\phi\left({x}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({t}^{{x}} −\mathrm{1}\right)\left({ln}\left(\mathrm{1}−{t}\right)\right)}{{tln}\left({t}\right)}{dt} \\ $$
Answered by mnjuly1970 last updated on 28/Nov/20
![solution: φ(x)=−∫_0 ^( 1) {((t^x −1)/(ln(t)))Σ_(n=1) ^∞ (t^(n−1) /n)}dx =−Σ_(n=1 ) ^∞ (1/n)∫_0 ^( 1) ((t^(x+n−1) −t^(n−1) )/(ln(t)))dt =−Σ_(n≥1) (1/n)[ln(x+n)−ln(n)] =−Σ_(n≥1) (1/n)ln(((x+n)/n))=−Σ_(n≥1) (1/n)ln(1+(x/n)) =−Σ_(n≥1) (1/n)Σ_(m≥1) (((((−x)/n))^m )/m)=Σ_(m≥1) (((−x)^m )/m)Σ_(n≥1) (1/n^(m+1) ) ∴ φ(x)=Σ_(m≥1) (((−x)^m ζ(m+1))/m) =(((−x)^1 )/1) ζ(2)+(x^2 /2)ζ(3)−(x^3 /3)ζ(4)+... ⇒((2φ(x))/x^2 )=ζ(3)−((2ζ(2))/x)−((2x)/3)ζ(4)+... ⇒2((φ(x))/x^2 )+(π^2 /(3x))=ζ(3)−((2x)/3)φζ(4)+... limit from both sides as x→0... lim_(x→0) (((2φ(x))/x^2 )+(π^2 /(3x)))=ζ(3) ✓✓ m.n.](https://www.tinkutara.com/question/Q123832.png)
$${solution}:\:\:\phi\left({x}\right)=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{{t}^{{x}} −\mathrm{1}}{{ln}\left({t}\right)}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{{n}−\mathrm{1}} }{{n}}\right\}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}^{{x}+{n}−\mathrm{1}} −{t}^{{n}−\mathrm{1}} }{{ln}\left({t}\right)}{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\left[{ln}\left({x}+{n}\right)−{ln}\left({n}\right)\right] \\ $$$$\:\:\:\:\:\:\:=−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}{ln}\left(\frac{{x}+{n}}{{n}}\right)=−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}{ln}\left(\mathrm{1}+\frac{{x}}{{n}}\right) \\ $$$$=−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{−{x}}{{n}}\right)^{{m}} }{{m}}=\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\left(−{x}\right)^{{m}} }{{m}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{{m}+\mathrm{1}} } \\ $$$$\therefore\:\phi\left({x}\right)=\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\left(−{x}\right)^{{m}} \:\zeta\left({m}+\mathrm{1}\right)}{{m}} \\ $$$$\:\:\:\:\:\:\:=\frac{\left(−{x}\right)^{\mathrm{1}} }{\mathrm{1}}\:\zeta\left(\mathrm{2}\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\zeta\left(\mathrm{3}\right)−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\zeta\left(\mathrm{4}\right)+… \\ $$$$\Rightarrow\frac{\mathrm{2}\phi\left({x}\right)}{{x}^{\mathrm{2}} }=\zeta\left(\mathrm{3}\right)−\frac{\mathrm{2}\zeta\left(\mathrm{2}\right)}{{x}}−\frac{\mathrm{2}{x}}{\mathrm{3}}\zeta\left(\mathrm{4}\right)+…\: \\ $$$$\Rightarrow\mathrm{2}\frac{\phi\left({x}\right)}{{x}^{\mathrm{2}} }+\frac{\pi^{\mathrm{2}} }{\mathrm{3}{x}}=\zeta\left(\mathrm{3}\right)−\frac{\mathrm{2}{x}}{\mathrm{3}}\phi\zeta\left(\mathrm{4}\right)+… \\ $$$${limit}\:{from}\:{both}\:\:{sides}\:\:{as}\:{x}\rightarrow\mathrm{0}… \\ $$$$\:{lim}_{{x}\rightarrow\mathrm{0}} \left(\frac{\mathrm{2}\phi\left({x}\right)}{{x}^{\mathrm{2}} }+\frac{\pi^{\mathrm{2}} }{\mathrm{3}{x}}\right)=\zeta\left(\mathrm{3}\right)\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}. \\ $$$$ \\ $$$$ \\ $$
