Question Number 189484 by mr W last updated on 17/Mar/23

Commented by mr W last updated on 17/Mar/23
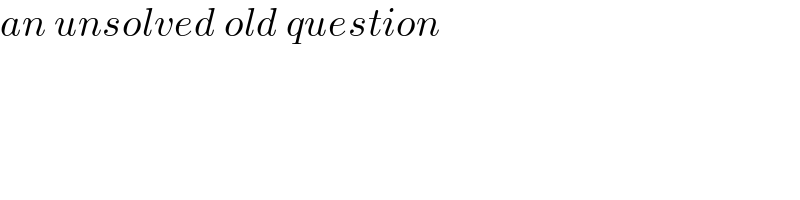
$${an}\:{unsolved}\:{old}\:{question} \\ $$
Answered by mr W last updated on 17/Mar/23

Commented by mr W last updated on 17/Mar/23
![a^→ +b^→ +c^→ =0 AY^(→) =a^→ +(3/4)b^→ BZ^(→) =−a^→ −(1/4)c^→ CX^(→) =(3/4)a^→ +c^→ say AP=ξ×AY, BP=η×BZ ξAY^(→) =a^→ +ηBZ^(→) ξ(a^→ +(3/4)b^→ )=a^→ +η(−a^→ −(1/4)c^→ ) (1−(ξ/4)−η)a^→ +(((3ξ)/4)−(η/4))c^→ =0 ⇒η=3ξ ⇒1−(ξ/4)−3ξ=0 ⇒ξ=(4/(13)), η=((12)/(13)) ⇒AP:PR:RY=4:8:1 [ABC]=Δ=52 [AYC]=(Δ/4) [APZ]=(4/(13))×(1/4)×[AYC]=(Δ/(52)) [CRY]=(([AYC])/(13))=(Δ/(52)) [PZCR]=(Δ/4)−2×(Δ/(52))=((11Δ)/(52)) [PQR]=Δ−3×(Δ/(52))−3×((11Δ)/(52))=(4/(13))[ABC] similary [APQX]=[BYRQ]=((11Δ)/(52)) ⇒green area=Δ−3×((11Δ)/(52))=((19Δ)/(52))=19 ✓ [PQR]=Δ−3×(Δ/(52))−3×((11Δ)/(52))=(4/(13))[ABC]](https://www.tinkutara.com/question/Q189487.png)
$$\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}+\overset{\rightarrow} {{c}}=\mathrm{0} \\ $$$$\overset{\rightarrow} {{AY}}=\overset{\rightarrow} {{a}}+\frac{\mathrm{3}}{\mathrm{4}}\overset{\rightarrow} {{b}} \\ $$$$\overset{\rightarrow} {{BZ}}=−\overset{\rightarrow} {{a}}−\frac{\mathrm{1}}{\mathrm{4}}\overset{\rightarrow} {{c}} \\ $$$$\overset{\rightarrow} {{CX}}=\frac{\mathrm{3}}{\mathrm{4}}\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{c}} \\ $$$${say}\:{AP}=\xi×{AY},\:{BP}=\eta×{BZ} \\ $$$$\xi\overset{\rightarrow} {{AY}}=\overset{\rightarrow} {{a}}+\eta\overset{\rightarrow} {{BZ}} \\ $$$$\xi\left(\overset{\rightarrow} {{a}}+\frac{\mathrm{3}}{\mathrm{4}}\overset{\rightarrow} {{b}}\right)=\overset{\rightarrow} {{a}}+\eta\left(−\overset{\rightarrow} {{a}}−\frac{\mathrm{1}}{\mathrm{4}}\overset{\rightarrow} {{c}}\right) \\ $$$$\left(\mathrm{1}−\frac{\xi}{\mathrm{4}}−\eta\right)\overset{\rightarrow} {{a}}+\left(\frac{\mathrm{3}\xi}{\mathrm{4}}−\frac{\eta}{\mathrm{4}}\right)\overset{\rightarrow} {{c}}=\mathrm{0} \\ $$$$\Rightarrow\eta=\mathrm{3}\xi \\ $$$$\Rightarrow\mathrm{1}−\frac{\xi}{\mathrm{4}}−\mathrm{3}\xi=\mathrm{0} \\ $$$$\Rightarrow\xi=\frac{\mathrm{4}}{\mathrm{13}},\:\eta=\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\Rightarrow{AP}:{PR}:{RY}=\mathrm{4}:\mathrm{8}:\mathrm{1} \\ $$$$\left[{ABC}\right]=\Delta=\mathrm{52} \\ $$$$\left[{AYC}\right]=\frac{\Delta}{\mathrm{4}} \\ $$$$\left[{APZ}\right]=\frac{\mathrm{4}}{\mathrm{13}}×\frac{\mathrm{1}}{\mathrm{4}}×\left[{AYC}\right]=\frac{\Delta}{\mathrm{52}} \\ $$$$\left[{CRY}\right]=\frac{\left[{AYC}\right]}{\mathrm{13}}=\frac{\Delta}{\mathrm{52}} \\ $$$$\left[{PZCR}\right]=\frac{\Delta}{\mathrm{4}}−\mathrm{2}×\frac{\Delta}{\mathrm{52}}=\frac{\mathrm{11}\Delta}{\mathrm{52}} \\ $$$$\left[{PQR}\right]=\Delta−\mathrm{3}×\frac{\Delta}{\mathrm{52}}−\mathrm{3}×\frac{\mathrm{11}\Delta}{\mathrm{52}}=\frac{\mathrm{4}}{\mathrm{13}}\left[{ABC}\right] \\ $$$${similary} \\ $$$$\left[{APQX}\right]=\left[{BYRQ}\right]=\frac{\mathrm{11}\Delta}{\mathrm{52}} \\ $$$$\Rightarrow{green}\:{area}=\Delta−\mathrm{3}×\frac{\mathrm{11}\Delta}{\mathrm{52}}=\frac{\mathrm{19}\Delta}{\mathrm{52}}=\mathrm{19}\:\checkmark \\ $$$$ \\ $$$$\left[{PQR}\right]=\Delta−\mathrm{3}×\frac{\Delta}{\mathrm{52}}−\mathrm{3}×\frac{\mathrm{11}\Delta}{\mathrm{52}}=\frac{\mathrm{4}}{\mathrm{13}}\left[{ABC}\right] \\ $$
