Question Number 124459 by Dwaipayan Shikari last updated on 03/Dec/20
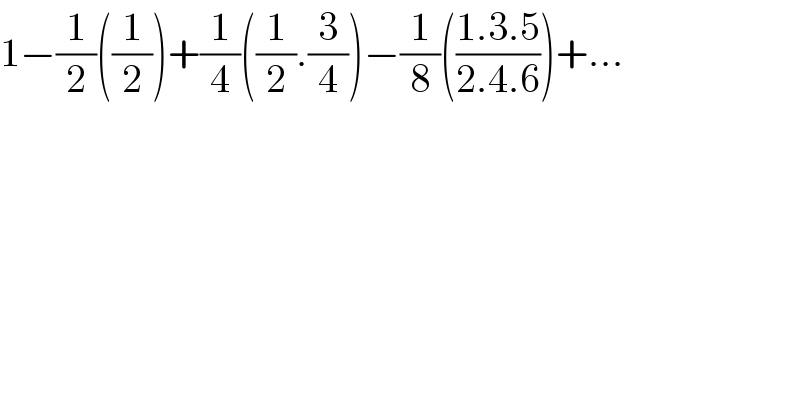
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}}{\mathrm{2}.\mathrm{4}.\mathrm{6}}\right)+… \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
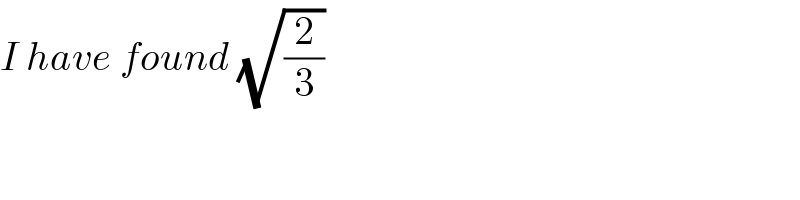
$${I}\:{have}\:{found}\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Answered by Olaf last updated on 03/Dec/20
![S = 1+Σ_(n=1) ^∞ (−1)^n (1/2^n )(((1×3×...(2n−1))/(2×4×...(2n)))) S = 1+Σ_(n=1) ^∞ (−1)^n (1/2^n )(((1×3×...(2n−1))/(2×4×...(2n)))) S = 1+Σ_(n=1) ^∞ (((−1)^n )/(2^n (2n)!))(1×3×...(2n−1))^2 S = 1+Σ_(n=1) ^∞ (((−1)^n )/(2^n (2n)!))[(((1×(2.1)×3×(2.2)×....(2n−1)×(2n))/((2.1)×(2.2)....(2n)))]^2 S = 1+Σ_(n=1) ^∞ (((−1)^n )/(2^n (2n)!))[(((2n)!)/((2^n n!))]^2 S = 1+Σ_(n=1) ^∞ (((−1)^n (2n)!)/(2^(3n) n!^2 )) S = 1+((√(2/3))−1) = (√(2/3))](https://www.tinkutara.com/question/Q124479.png)
$$\mathrm{S}\:=\:\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\frac{\mathrm{1}×\mathrm{3}×…\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{2}×\mathrm{4}×…\left(\mathrm{2}{n}\right)}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\frac{\mathrm{1}×\mathrm{3}×…\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{2}×\mathrm{4}×…\left(\mathrm{2}{n}\right)}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left(\mathrm{2}{n}\right)!}\left(\mathrm{1}×\mathrm{3}×…\left(\mathrm{2}{n}−\mathrm{1}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{S}\:=\:\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left(\mathrm{2}{n}\right)!}\left[\frac{\left(\mathrm{1}×\left(\mathrm{2}.\mathrm{1}\right)×\mathrm{3}×\left(\mathrm{2}.\mathrm{2}\right)×….\left(\mathrm{2}{n}−\mathrm{1}\right)×\left(\mathrm{2}{n}\right)\right.}{\left(\mathrm{2}.\mathrm{1}\right)×\left(\mathrm{2}.\mathrm{2}\right)….\left(\mathrm{2}{n}\right)}\right]^{\mathrm{2}} \\ $$$$\mathrm{S}\:=\:\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left(\mathrm{2}{n}\right)!}\left[\frac{\left(\mathrm{2}{n}\right)!}{\left(\mathrm{2}^{{n}} {n}!\right.}\right]^{\mathrm{2}} \\ $$$$\mathrm{S}\:=\:\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{3}{n}} {n}!^{\mathrm{2}} } \\ $$$$\mathrm{S}\:=\:\mathrm{1}+\left(\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}−\mathrm{1}\right)\:=\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20
$${very}\:{nice}\:{sir}\:{olaf} \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20

$${Thanking}\:{you} \\ $$
