Question Number 125049 by bramlexs22 last updated on 08/Dec/20
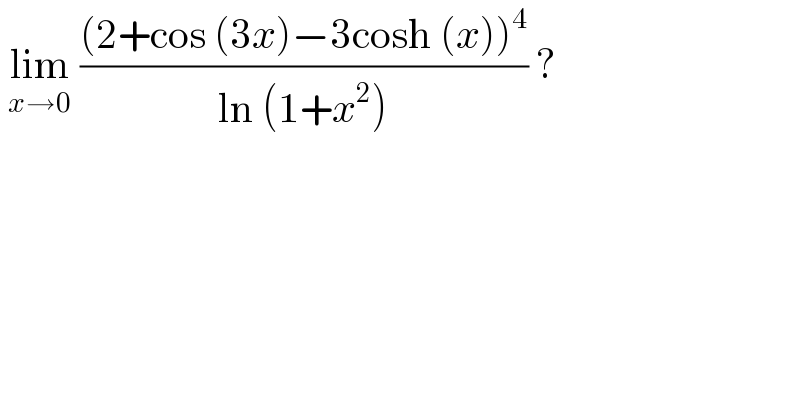
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}+\mathrm{cos}\:\left(\mathrm{3}{x}\right)−\mathrm{3cosh}\:\left({x}\right)\right)^{\mathrm{4}} }{\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:? \\ $$
Answered by Olaf last updated on 08/Dec/20
![lim_(x→0) (((2+cos3x−3coshx)^4 )/(ln(1+x^2 ))) = lim_(x→0) (([2+(1−((9x^2 )/2))−3(1+(x^2 /2))]^4 )/(x^2 −(x^4 /2)+(x^6 /3)−(x^8 /4))) = lim_(x→0) ((6^4 x^8 )/(x^2 −(x^4 /2)+(x^6 /3)−(x^8 /4))) = lim_(x→0) 6^4 x^6 = 0](https://www.tinkutara.com/question/Q125061.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}+\mathrm{cos3}{x}−\mathrm{3cosh}{x}\right)^{\mathrm{4}} }{\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left[\mathrm{2}+\left(\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\right)−\mathrm{3}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\right]^{\mathrm{4}} }{{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{2}}+\frac{{x}^{\mathrm{6}} }{\mathrm{3}}−\frac{{x}^{\mathrm{8}} }{\mathrm{4}}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6}^{\mathrm{4}} {x}^{\mathrm{8}} }{{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{2}}+\frac{{x}^{\mathrm{6}} }{\mathrm{3}}−\frac{{x}^{\mathrm{8}} }{\mathrm{4}}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{6}^{\mathrm{4}} {x}^{\mathrm{6}} \:=\:\mathrm{0} \\ $$
