Question Number 125336 by mnjuly1970 last updated on 10/Dec/20
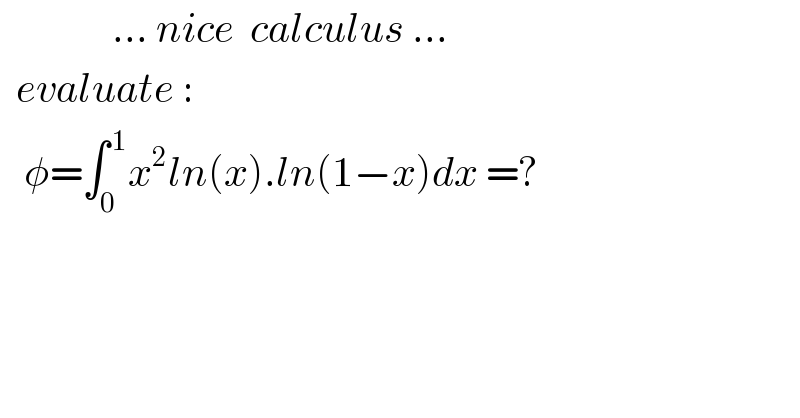
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{calculus}\:… \\ $$$$\:\:{evaluate}\:: \\ $$$$\:\:\:\phi=\int_{\mathrm{0}\:} ^{\:\mathrm{1}} {x}^{\mathrm{2}} {ln}\left({x}\right).{ln}\left(\mathrm{1}−{x}\right){dx}\:=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 10/Dec/20
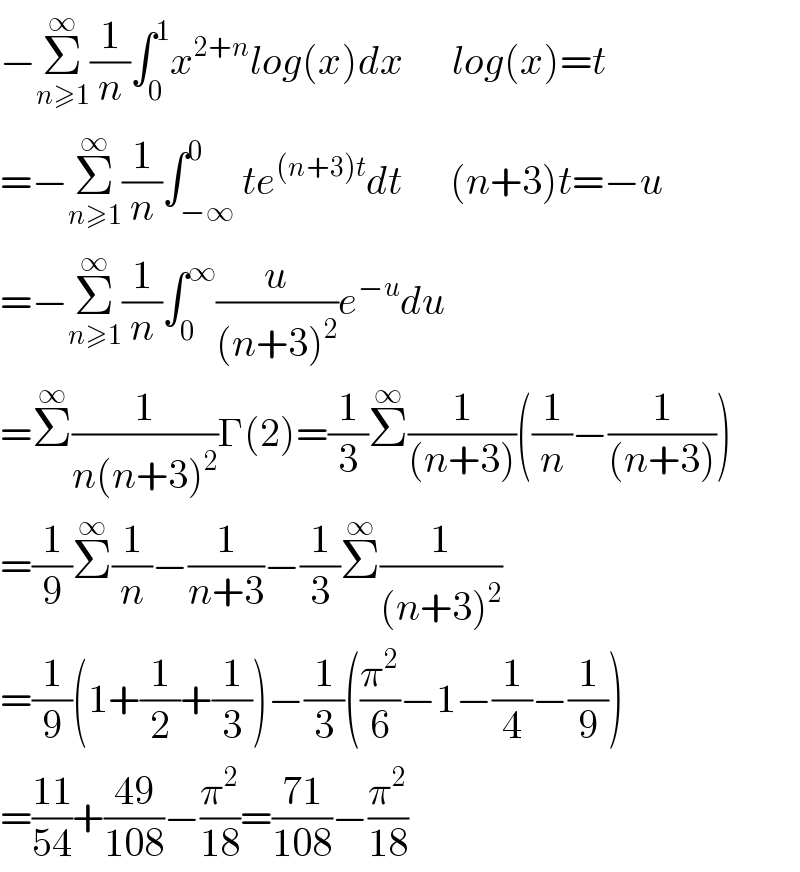
$$−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}+{n}} {log}\left({x}\right){dx}\:\:\:\:\:\:{log}\left({x}\right)={t} \\ $$$$=−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{−\infty} ^{\mathrm{0}} {te}^{\left({n}+\mathrm{3}\right){t}} {dt}\:\:\:\:\:\:\left({n}+\mathrm{3}\right){t}=−{u} \\ $$$$=−\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} \frac{{u}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }{e}^{−{u}} {du} \\ $$$$=\overset{\infty} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} }\Gamma\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{3}}\overset{\infty} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\overset{\infty} {\sum}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\overset{\infty} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{9}}\right) \\ $$$$=\frac{\mathrm{11}}{\mathrm{54}}+\frac{\mathrm{49}}{\mathrm{108}}−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}=\frac{\mathrm{71}}{\mathrm{108}}−\frac{\pi^{\mathrm{2}} }{\mathrm{18}} \\ $$
Commented by mnjuly1970 last updated on 10/Dec/20
$$\:\:{very}\:{nice}\:{solution}. \\ $$$${thanks}\:{alot}… \\ $$
Commented by Dwaipayan Shikari last updated on 10/Dec/20
$${With}\:{pleasure}\:{sir}! \\ $$
Answered by Olaf last updated on 10/Dec/20
![Let I_n = ∫_0 ^1 x^n lnxdx, n∈N I_n = [(x^(n+1) /(n+1))lnx]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1)).(dx/x) I_n = −(1/(n+1))∫_0 ^1 x^n dx I_n = −(1/(n+1))[(x^(n+1) /(n+1))]_0 ^1 = −(1/((n+1)^2 )) φ = ∫_0 ^1 x^2 lnxln(1−x)dx φ = ∫_0 ^1 x^2 lnxΣ_(n=1) ^∞ (x^n /n)dx φ = Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^(n+2) lnxdx φ = Σ_(n=1) ^∞ (I_(n+2) /n) φ = −Σ_(n=1) ^∞ (1/(n(n+3)^2 )) φ = −(1/9)Σ_(n=1) ^∞ [(1/n)−(1/(n+3))−(3/((n+3)^2 ))] φ = −(1/9)Σ_(n=1) ^∞ [(1/n)−(1/(n+3))]+(1/3)Σ_(n=1) ^∞ (1/((n+3)^2 )) φ = −(1/9)[1+(1/2)+(1/3)]+(1/3)[Σ_(n=1) ^∞ (1/n^2 )−(1+(1/4)+(1/9))] φ = −(1/9)[((11)/6)]+(1/3)[(π^2 /6)−((49)/(36))] φ = (π^2 /(18))−((71)/(108))](https://www.tinkutara.com/question/Q125349.png)
$$\mathrm{Let}\:\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{ln}{xdx},\:{n}\in\mathbb{N} \\ $$$$\mathrm{I}_{{n}} \:=\:\left[\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mathrm{ln}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}.\frac{{dx}}{{x}} \\ $$$$\mathrm{I}_{{n}} \:=\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {dx} \\ $$$$\mathrm{I}_{{n}} \:=\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\left[\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \mathrm{ln}{x}\mathrm{ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \mathrm{ln}{x}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}{dx} \\ $$$$\phi\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+\mathrm{2}} \mathrm{ln}{xdx} \\ $$$$\phi\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{I}_{{n}+\mathrm{2}} }{{n}} \\ $$$$\phi\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\phi\:=\:−\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}−\frac{\mathrm{3}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }\right] \\ $$$$\phi\:=\:−\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right]+\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\phi\:=\:−\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\right]+\frac{\mathrm{1}}{\mathrm{3}}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{9}}\right)\right] \\ $$$$\phi\:=\:−\frac{\mathrm{1}}{\mathrm{9}}\left[\frac{\mathrm{11}}{\mathrm{6}}\right]+\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{49}}{\mathrm{36}}\right] \\ $$$$\phi\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{18}}−\frac{\mathrm{71}}{\mathrm{108}} \\ $$
Commented by mnjuly1970 last updated on 10/Dec/20
$${grateful}\:{mr}\:{olaf}… \\ $$
