Question Number 125918 by I want to learn more last updated on 15/Dec/20
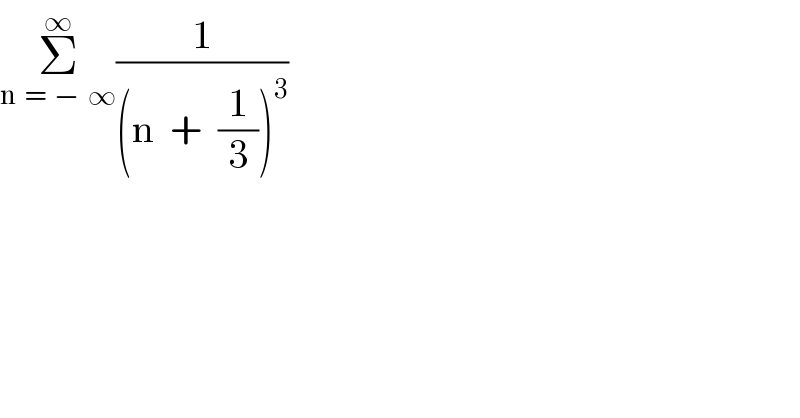
$$\underset{\mathrm{n}\:\:=\:\:−\:\:\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$
Answered by mindispower last updated on 15/Dec/20
![f(z)=((πcot(πz))/((z+(1/3))^3 )),over Re^(iθ) ,θ∈[0,2π];R→∞ lim_(R→∞) ∫_C f(z)dz=2iπRes(f,C)=0 ∣cot(πz)∣<M,∣z∣→0 (1/((z+(1/3))^3 ))→0 when ∣z∣→∞ pols of f are −(1/3),order 3 k∈Z order 1 Res(f,k)=(1/((k+(1/3))^3 )) Res(f,−(1/3))=(1/2)(∂/∂z^2 ).πcot(πz) =(1/2)[2π^3 (1+cot^2 (πz))cot(πz))∣z=−(1/3) =π^3 ((4/3))(−(1/( (√3)))) =((−4π^3 )/(3(√3))) Σ_(k∈Z) ^ Res(f,k)+Res(f,−(1/3))=0 ⇒Σres(f,k)=−Res(f,−(1/3))=((4π^3 )/(3(√3)))](https://www.tinkutara.com/question/Q125920.png)
$${f}\left({z}\right)=\frac{\pi{cot}\left(\pi{z}\right)}{\left({z}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} },{over}\:{Re}^{{i}\theta} ,\theta\in\left[\mathrm{0},\mathrm{2}\pi\right];{R}\rightarrow\infty \\ $$$$\underset{{R}\rightarrow\infty} {\mathrm{lim}}\int_{{C}} {f}\left({z}\right){dz}=\mathrm{2}{i}\pi{Res}\left({f},{C}\right)=\mathrm{0} \\ $$$$\mid{cot}\left(\pi{z}\right)\mid<{M},\mid{z}\mid\rightarrow\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\left({z}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} }\rightarrow\mathrm{0}\:{when}\:\mid{z}\mid\rightarrow\infty \\ $$$${pols}\:{of}\:{f}\:{are}\:−\frac{\mathrm{1}}{\mathrm{3}},{order}\:\mathrm{3}\: \\ $$$${k}\in\mathbb{Z}\:{order}\:\mathrm{1} \\ $$$${Res}\left({f},{k}\right)=\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$$${Res}\left({f},−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\frac{\partial}{\partial{z}^{\mathrm{2}} }.\pi{cot}\left(\pi{z}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{2}\pi^{\mathrm{3}} \left(\mathrm{1}+{cot}^{\mathrm{2}} \left(\pi{z}\right)\right){cot}\left(\pi{z}\right)\right)\mid{z}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\pi^{\mathrm{3}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{−\mathrm{4}\pi^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\underset{{k}\in\mathbb{Z}} {\overset{} {\sum}}{Res}\left({f},{k}\right)+{Res}\left({f},−\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\Rightarrow\Sigma{res}\left({f},{k}\right)=−{Res}\left({f},−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{4}\pi^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by I want to learn more last updated on 15/Dec/20
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by mnjuly1970 last updated on 16/Dec/20

Commented by I want to learn more last updated on 16/Dec/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}.\:\mathrm{But}\:\mathrm{sir},\:\mathrm{where}\:\mathrm{can}\:\mathrm{i}\:\mathrm{learn}\:\mathrm{summation}\:\mathrm{like}\:\mathrm{this}. \\ $$$$\mathrm{please}.\:\mathrm{Tell}\:\mathrm{me}\:\mathrm{a}\:\mathrm{book}\:\mathrm{to}\:\mathrm{download}.\:\mathrm{please}. \\ $$
Commented by mnjuly1970 last updated on 16/Dec/20

$$\:\:\:\:\:\:{thank}\:{you}\:{so}\:{much}\:{master}.. \\ $$$$\:\:\:\:\:\mathrm{1}.\:{advanced}\:{calculus}\:…\left\{_{\mathrm{2}.{Ruel}−\:{chuchill}} ^{\mathrm{1}.{M}\:{urray}−\:{spiegel}} \right. \\ $$$$\:\:\:\:\:\mathrm{2}.\:{complex}\:\:{analysis}\:..\left({Ruel}−\:{churchill}\right) \\ $$$$\:\:\:\:\:\: \\ $$
Commented by I want to learn more last updated on 20/Dec/20
$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
