Question Number 127042 by benjo_mathlover last updated on 26/Dec/20
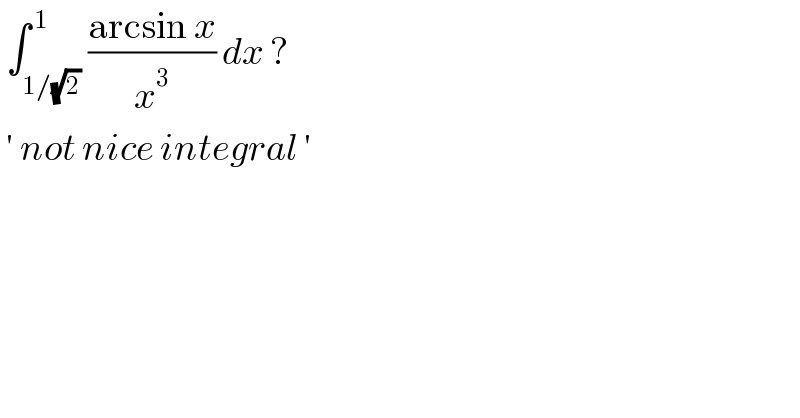
$$\:\int_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{\:\mathrm{1}} \frac{\mathrm{arcsin}\:{x}}{{x}^{\mathrm{3}} }\:{dx}\:? \\ $$$$\:'\:{not}\:{nice}\:{integral}\:'\: \\ $$
Commented by liberty last updated on 26/Dec/20
��������
Answered by liberty last updated on 26/Dec/20
![L=∫_(1/(√2)) ^( 1) ((arcsin x)/x^3 ) dx = (−((arcsin x)/(2x^2 )))_(1/(√2)) ^1 +(1/2)∫_(1/(√2)) ^( 1) (dx/(x^2 (√(1−x^2 )))) L= 0 + (1/2)∫_(1/(√2)) ^( 1) (dx/(x^2 (√(1−x^2 )))) [ x = sin h ] L=(1/2)∫_(π/4) ^( π/2) ((cos h dh)/(sin^2 h (√(1−sin^2 h)))) = (1/2)∫_(π/4) ^( π/2) cosec^2 h dh L = −(1/2) [cot h ]_(π/4) ^(π/2) = (1/2)](https://www.tinkutara.com/question/Q127044.png)
$${L}=\int_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{\:\mathrm{1}} \frac{\mathrm{arcsin}\:{x}}{{x}^{\mathrm{3}} }\:{dx}\:=\:\left(−\frac{\mathrm{arcsin}\:{x}}{\mathrm{2}{x}^{\mathrm{2}} }\right)_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{\:\mathrm{1}} \frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${L}=\:\mathrm{0}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{\:\mathrm{1}} \frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\:\left[\:{x}\:=\:\mathrm{sin}\:{h}\:\right]\: \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{4}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{cos}\:{h}\:{dh}}{\mathrm{sin}\:^{\mathrm{2}} {h}\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {h}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{4}} ^{\:\pi/\mathrm{2}} \:\mathrm{cosec}\:^{\mathrm{2}} {h}\:{dh} \\ $$$${L}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:\left[\mathrm{cot}\:{h}\:\right]_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 27/Dec/20
![I =∫_(1/( (√2))) ^1 ((arcsinx)/x^3 )dx by parts u^′ =x^(−3) and v=arcsinx ⇒ I =[−(1/(2x^2 ))arcsinx]_(1/( (√2))) ^1 +∫_(1/( (√2))) ^1 (1/(2x^2 ))(dx/( (√(1−x^2 )))) =−(1/2){(π/2)−2×(π/4)}+(1/2)∫_(1/( (√2))) ^1 (dx/(x^2 (√(1−x^2 ))))=(1/2)∫_(1/( (√2))) ^1 (dx/(x^2 (√(1−x^2 )))) changement x=sint give ∫_(1/( (√2))) ^1 (dx/(x^2 (√(1−x^2 ))))=∫_(π/4) ^(π/2) ((cost dt)/(sin^2 t cost)) =2∫_(π/4) ^(π/2) (dt/(1−cos(2t)))=_(2t=α) ∫_(π/2) ^π (dα/(1−cosα)) =_(tan((α/2))=z) =∫_1 ^∞ ((2dz)/((1+z^2 )(1−((1−z^2 )/(1+z^2 ))))) =2∫_1 ^∞ (dz/(1+z^2 −1+z^2 )) =∫_1 ^∞ (dz/z^2 )=[−(1/z)]_1 ^∞ =1 ⇒ ★I =(1/2)★](https://www.tinkutara.com/question/Q127167.png)
$$\mathrm{I}\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{arcsinx}}{\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\mathrm{x}^{−\mathrm{3}} \:\mathrm{and}\:\mathrm{v}=\mathrm{arcsinx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\left[−\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\mathrm{arcsinx}\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} +\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\pi}{\mathrm{2}}−\mathrm{2}×\frac{\pi}{\mathrm{4}}\right\}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{changement}\:\mathrm{x}=\mathrm{sint}\:\mathrm{give}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cost}\:\mathrm{dt}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{cost}} \\ $$$$=\mathrm{2}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}=_{\mathrm{2t}=\alpha} \:\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\:\frac{\mathrm{d}\alpha}{\mathrm{1}−\mathrm{cos}\alpha}\:=_{\mathrm{tan}\left(\frac{\alpha}{\mathrm{2}}\right)=\mathrm{z}} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{2dz}}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\right)}\:=\mathrm{2}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} −\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} }=\left[−\frac{\mathrm{1}}{\mathrm{z}}\right]_{\mathrm{1}} ^{\infty} =\mathrm{1}\:\Rightarrow \\ $$$$\bigstar\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\bigstar \\ $$
