Menu Close

Solve-in-C-1-iz-1-iz-n-e-i-n-n-R-n-N-

Tinku Tara 0 Comments
Pin




Question Number 127081 by slahadjb last updated on 26/Dec/20
Solve in C (((1+iz)/(1−iz)))^n =e_ ^(iθ_n ) θ_n ∈ R n ∈ N
$${Solve}\:{in}\:\mathbb{C} \\ $$$$\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right)^{{n}} ={e}_{} ^{{i}\theta_{{n}} } \\ $$$$\theta_{{n}} \:\in\:\mathbb{R} \\ $$$${n}\:\in\:\mathbb{N} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Dec/20
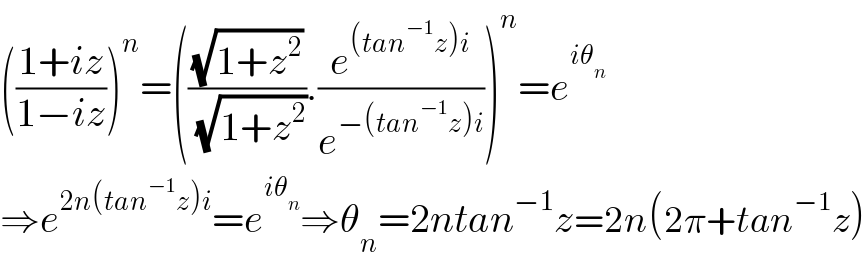
(((1+iz)/(1−iz)))^n =(((√(1+z^2 ))/( (√(1+z^2 )))).(e^((tan^(−1) z)i) /e^(−(tan^(−1) z)i) ))^n =e^(iθ_n ) ⇒e^(2n(tan^(−1) z)i) =e^(iθ_n ) ⇒θ_n =2ntan^(−1) z=2n(2π+tan^(−1) z)
$$\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right)^{{n}} =\left(\frac{\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}.\frac{{e}^{\left({tan}^{−\mathrm{1}} {z}\right){i}} }{{e}^{−\left({tan}^{−\mathrm{1}} {z}\right){i}} }\right)^{{n}} ={e}^{{i}\theta_{{n}} } \\ $$$$\Rightarrow{e}^{\mathrm{2}{n}\left({tan}^{−\mathrm{1}} {z}\right){i}} ={e}^{{i}\theta_{{n}} } \Rightarrow\theta_{{n}} =\mathrm{2}{ntan}^{−\mathrm{1}} {z}=\mathrm{2}{n}\left(\mathrm{2}\pi+{tan}^{−\mathrm{1}} {z}\right) \\ $$
Commented by Olaf last updated on 26/Dec/20
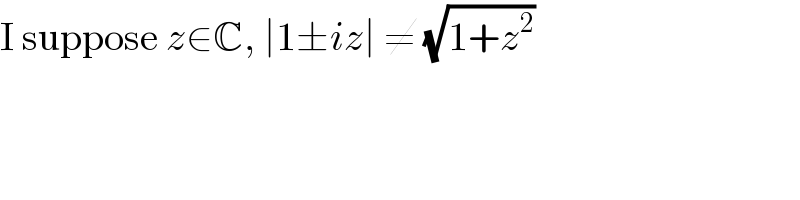
I suppose z∈C, ∣1±iz∣ ≠ (√(1+z^2 ))
$$\mathrm{I}\:\mathrm{suppose}\:{z}\in\mathbb{C},\:\mid\mathrm{1}\pm{iz}\mid\:\neq\:\sqrt{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$
Commented by Escritor last updated on 26/Dec/20
Excellent
$${Excellent} \\ $$
Answered by mathmax by abdo last updated on 26/Dec/20
(((1+iz)/(1−iz)))^n =e^(iθ_n ) =e^(i(θ_n +2kπ)) ⇒((1+iz_k )/(1−iz_k )) =e^(i(((θ_n +2kπ)/n))) ⇒ 1+iz_k =e^(i(((θ_n +2kπ)/n))) −ie^(i(((θ_n +2kπ)/n))) z_k ⇒i(1+e^(i(((θ_n +2kπ)/n))) )z_k =e^(i(((θ_n +2kπ)/n))) −1 ⇒ z_k =−((1−e^(i(((θ_n +2kπ)/n))) )/(1+e^(i(((θ_n +2kπ)/n))) )) =−((1−cos(((θ_n +2kπ)/n))−isin(((θ_n +2kπ)/n)))/(1+cos(((θ_n +2kπ)/n))+isin(((θ_n +2kπ)/n)))) =−((2sin^2 (((θ_n +2kπ)/(2n)))−2isin(((θ_n +2kπ)/(2n)))cos(((θ_n +2kπ)/(2n))))/(2cos^2 (((θ_n +2kπ)/(2n)))+2isin(((θ_n +2kπ)/(2n)))cos(((θ_n +2kπ)/(2n))))) −((−isin(((θ_n +2kπ)/(2n)))e^(i(((θ_n +2kπ)/(2n)))) )/(cos(((θ_n +2kπ)/(2n))) e^(i(((θ_n +2kπ)/(2n)))) ))=itan(((θ_n +2kπ)/(2n))) with k∈[[0,n−1]]
$$\left(\frac{\mathrm{1}+\mathrm{iz}}{\mathrm{1}−\mathrm{iz}}\right)^{\mathrm{n}} \:=\mathrm{e}^{\mathrm{i}\theta_{\mathrm{n}} } \:=\mathrm{e}^{\mathrm{i}\left(\theta_{\mathrm{n}} +\mathrm{2k}\pi\right)} \:\Rightarrow\frac{\mathrm{1}+\mathrm{iz}_{\mathrm{k}} }{\mathrm{1}−\mathrm{iz}_{\mathrm{k}} }\:=\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} \:\Rightarrow \\ $$$$\mathrm{1}+\mathrm{iz}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} −\mathrm{ie}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} \:\mathrm{z}_{\mathrm{k}} \:\Rightarrow\mathrm{i}\left(\mathrm{1}+\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} \right)\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} −\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{k}} =−\frac{\mathrm{1}−\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} }{\mathrm{1}+\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} }\:=−\frac{\mathrm{1}−\mathrm{cos}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)−\mathrm{isin}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)}{\mathrm{1}+\mathrm{cos}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)+\mathrm{isin}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{n}}\right)} \\ $$$$=−\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)−\mathrm{2isin}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)\mathrm{cos}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)}{\mathrm{2cos}^{\mathrm{2}} \left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)+\mathrm{2isin}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)\mathrm{cos}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)} \\ $$$$−\frac{−\mathrm{isin}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)} }{\mathrm{cos}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)\:\mathrm{e}^{\mathrm{i}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)} }=\mathrm{itan}\left(\frac{\theta_{\mathrm{n}} +\mathrm{2k}\pi}{\mathrm{2n}}\right)\:\:\mathrm{with}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{n}−\mathrm{1}\right]\right] \\ $$
Commented by slahadjb last updated on 28/Dec/20
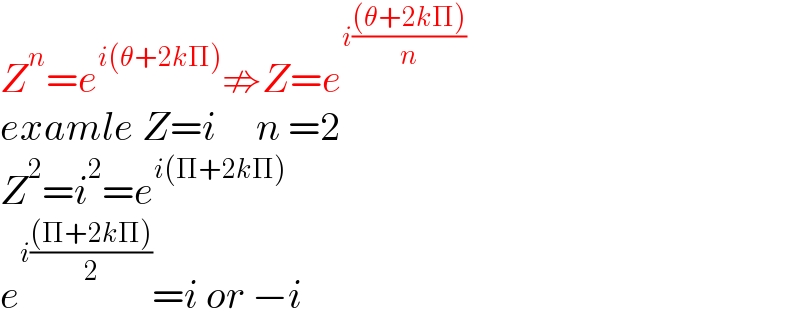
Z^n =e^(i(θ+2kΠ)) ⇏Z=e^(i(((θ+2kΠ))/n)) examle Z=i n =2 Z^2 =i^2 =e^(i(Π+2kΠ)) e^(i(((Π+2kΠ))/2)) =i or −i
$${Z}^{{n}} ={e}^{{i}\left(\theta+\mathrm{2}{k}\Pi\right)} \nRightarrow{Z}={e}^{{i}\frac{\left(\theta+\mathrm{2}{k}\Pi\right)}{{n}}} \\ $$$${examle}\:{Z}={i}\:\:\:\:\:{n}\:=\mathrm{2} \\ $$$${Z}^{\mathrm{2}} ={i}^{\mathrm{2}} ={e}^{{i}\left(\Pi+\mathrm{2}{k}\Pi\right)} \\ $$$${e}^{{i}\frac{\left(\Pi+\mathrm{2}{k}\Pi\right)}{\mathrm{2}}} ={i}\:{or}\:−{i} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *