Question Number 127132 by mathocean1 last updated on 27/Dec/20
![knowing that 7^(3k+1) ≡7[mod 9] ;k ∈ N. show that 2005^(2005) ≡7[mod 9]](https://www.tinkutara.com/question/Q127132.png)
$${knowing}\:{that}\:\mathrm{7}^{\mathrm{3}{k}+\mathrm{1}} \equiv\mathrm{7}\left[{mod}\:\mathrm{9}\right]\:;{k}\:\in\:\mathbb{N}. \\ $$$${show}\:{that}\:\mathrm{2005}^{\mathrm{2005}} \equiv\mathrm{7}\left[{mod}\:\mathrm{9}\right] \\ $$
Answered by JDamian last updated on 27/Dec/20
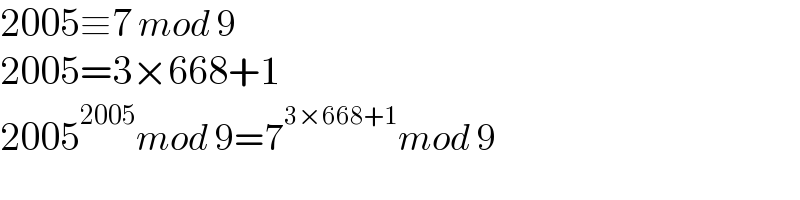
$$\mathrm{2005}\equiv\mathrm{7}\:{mod}\:\mathrm{9} \\ $$$$\mathrm{2005}=\mathrm{3}×\mathrm{668}+\mathrm{1} \\ $$$$\mathrm{2005}^{\mathrm{2005}} {mod}\:\mathrm{9}=\mathrm{7}^{\mathrm{3}×\mathrm{668}+\mathrm{1}} {mod}\:\mathrm{9} \\ $$
