Question Number 127157 by kaivan.ahmadi last updated on 27/Dec/20
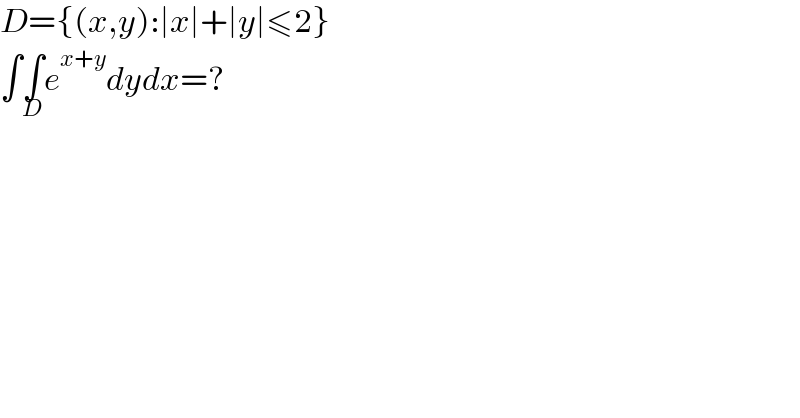
$${D}=\left\{\left({x},{y}\right):\mid{x}\mid+\mid{y}\mid\leqslant\mathrm{2}\right\} \\ $$$$\int\underset{{D}} {\int}{e}^{{x}+{y}} {dydx}=? \\ $$
Answered by Ar Brandon last updated on 27/Dec/20
![D={(x, y) : ∣x∣+∣y∣≤2} = { ((x+y≤2)),((x−y≤2)),((−x+y≤2)),((−x−y≤2)) :} I=∫_0 ^2 ∫_(x−2) ^(2−x) e^(x+y) dydx+∫_(−2) ^0 ∫_(−x−2) ^(x+2) e^(x+y) dydx =∫_0 ^2 [e^(x+y) ]_(x−2) ^(2−x) dx+∫_(−2) ^0 [e^(x+y) ]_(−x−2) ^(x+2) dx =∫_0 ^2 [e^2 −e^(2x−2) ]dx+∫_(−2) ^0 [e^(2x+2) −e^(−2) ]dx =[xe^2 −(1/2)e^(2x−2) ]_0 ^2 +[(1/2)e^(2x+2) −xe^(−2) ]_(−2) ^0 =[(2e^2 −(1/2)e^2 )+(1/2)e^(−2) ]+[(1/2)e^2 −((1/2)e^(−2) −2e^(−2) )] =2e^2 +2e^(−2) =2(e^2 +e^(−2) )](https://www.tinkutara.com/question/Q127163.png)
$$\mathrm{D}=\left\{\left(\mathrm{x},\:\mathrm{y}\right)\::\:\mid\mathrm{x}\mid+\mid\mathrm{y}\mid\leqslant\mathrm{2}\right\} \\ $$$$\:\:\:\:=\begin{cases}{\mathrm{x}+\mathrm{y}\leqslant\mathrm{2}}\\{\mathrm{x}−\mathrm{y}\leqslant\mathrm{2}}\\{−\mathrm{x}+\mathrm{y}\leqslant\mathrm{2}}\\{−\mathrm{x}−\mathrm{y}\leqslant\mathrm{2}}\end{cases} \\ $$$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{x}−\mathrm{2}} ^{\mathrm{2}−\mathrm{x}} \mathrm{e}^{\mathrm{x}+\mathrm{y}} \mathrm{dydx}+\int_{−\mathrm{2}} ^{\mathrm{0}} \int_{−\mathrm{x}−\mathrm{2}} ^{\mathrm{x}+\mathrm{2}} \mathrm{e}^{\mathrm{x}+\mathrm{y}} \mathrm{dydx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left[\mathrm{e}^{\mathrm{x}+\mathrm{y}} \right]_{\mathrm{x}−\mathrm{2}} ^{\mathrm{2}−\mathrm{x}} \mathrm{dx}+\int_{−\mathrm{2}} ^{\mathrm{0}} \left[\mathrm{e}^{\mathrm{x}+\mathrm{y}} \right]_{−\mathrm{x}−\mathrm{2}} ^{\mathrm{x}+\mathrm{2}} \mathrm{dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left[\mathrm{e}^{\mathrm{2}} −\mathrm{e}^{\mathrm{2x}−\mathrm{2}} \right]\mathrm{dx}+\int_{−\mathrm{2}} ^{\mathrm{0}} \left[\mathrm{e}^{\mathrm{2x}+\mathrm{2}} −\mathrm{e}^{−\mathrm{2}} \right]\mathrm{dx} \\ $$$$\:\:\:=\left[\mathrm{xe}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}−\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{2}} +\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}+\mathrm{2}} −\mathrm{xe}^{−\mathrm{2}} \right]_{−\mathrm{2}} ^{\mathrm{0}} \\ $$$$\:\:\:=\left[\left(\mathrm{2e}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}} \right]+\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}} −\mathrm{2e}^{−\mathrm{2}} \right)\right] \\ $$$$\:\:\:=\mathrm{2e}^{\mathrm{2}} +\mathrm{2e}^{−\mathrm{2}} =\mathrm{2}\left(\mathrm{e}^{\mathrm{2}} +\mathrm{e}^{−\mathrm{2}} \right) \\ $$
Answered by mathmax by abdo last updated on 27/Dec/20
![∣x∣+∣y∣≤2 ⇒−2≤x ≤2 also ∣y∣≤2−∣x∣ ⇒∣x∣−2≤y≤2−∣x∣ ⇒ ∫∫_D e^(x+y) dx dy =∫_(−2) ^2 ∫_(∣x∣−2) ^(2−∣x∣) e^(x+y) dy dx =∫_(−2) ^2 (∫_(∣x∣−2) ^(2−∣x∣) e^y dy)e^x dx [we have ∫_(∣x∣−2) ^(2−∣x∣) e^y dy =[e^y ]_(∣x∣−2) ^(2−∣x∣) =e^(2−∣x∣) −e^(∣x∣−2) ⇒ I =∫_(−2) ^2 e^(2−∣x∣) dx−∫_(−2) ^2 e^(∣x∣−2) dx =2e^2 ∫_0 ^2 e^(−x) dx−2e^(−2) ∫_0 ^2 e^x dx =2e^2 [−e^(−x) ]_0 ^2 [−2e^(−2) [e^x ]_0 ^2 =2e^2 (1−e^(−2) )−2e^(−2) (e^2 −1) =2e^2 −2−2+2e^(−2) =2e^2 +2e^(−2) −4](https://www.tinkutara.com/question/Q127201.png)
$$\mid\mathrm{x}\mid+\mid\mathrm{y}\mid\leqslant\mathrm{2}\:\Rightarrow−\mathrm{2}\leqslant\mathrm{x}\:\:\leqslant\mathrm{2}\:\:\mathrm{also}\:\:\mid\mathrm{y}\mid\leqslant\mathrm{2}−\mid\mathrm{x}\mid\:\Rightarrow\mid\mathrm{x}\mid−\mathrm{2}\leqslant\mathrm{y}\leqslant\mathrm{2}−\mid\mathrm{x}\mid\:\Rightarrow \\ $$$$\int\int_{\mathrm{D}} \mathrm{e}^{\mathrm{x}+\mathrm{y}} \:\mathrm{dx}\:\mathrm{dy}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \:\int_{\mid\mathrm{x}\mid−\mathrm{2}} ^{\mathrm{2}−\mid\mathrm{x}\mid} \:\mathrm{e}^{\mathrm{x}+\mathrm{y}} \mathrm{dy}\:\mathrm{dx} \\ $$$$=\int_{−\mathrm{2}} ^{\mathrm{2}} \:\left(\int_{\mid\mathrm{x}\mid−\mathrm{2}} ^{\mathrm{2}−\mid\mathrm{x}\mid} \:\mathrm{e}^{\mathrm{y}} \:\mathrm{dy}\right)\mathrm{e}^{\mathrm{x}} \:\mathrm{dx}\:\left[\mathrm{we}\:\mathrm{have}\right. \\ $$$$\int_{\mid\mathrm{x}\mid−\mathrm{2}} ^{\mathrm{2}−\mid\mathrm{x}\mid} \:\:\mathrm{e}^{\mathrm{y}} \:\mathrm{dy}\:=\left[\mathrm{e}^{\mathrm{y}} \right]_{\mid\mathrm{x}\mid−\mathrm{2}} ^{\mathrm{2}−\mid\mathrm{x}\mid} \:=\mathrm{e}^{\mathrm{2}−\mid\mathrm{x}\mid} −\mathrm{e}^{\mid\mathrm{x}\mid−\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2}−\mid\mathrm{x}\mid} \mathrm{dx}−\int_{−\mathrm{2}} ^{\mathrm{2}} \:\mathrm{e}^{\mid\mathrm{x}\mid−\mathrm{2}} \:\mathrm{dx} \\ $$$$=\mathrm{2e}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}−\mathrm{2e}^{−\mathrm{2}} \:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{e}^{\mathrm{x}} \:\mathrm{dx} \\ $$$$=\mathrm{2e}^{\mathrm{2}} \left[−\mathrm{e}^{−\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{2}} \left[−\mathrm{2e}^{−\mathrm{2}} \left[\mathrm{e}^{\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{2}} \:=\mathrm{2e}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{e}^{−\mathrm{2}} \right)−\mathrm{2e}^{−\mathrm{2}} \left(\mathrm{e}^{\mathrm{2}} −\mathrm{1}\right)\right. \\ $$$$=\mathrm{2e}^{\mathrm{2}} −\mathrm{2}−\mathrm{2}+\mathrm{2e}^{−\mathrm{2}} \:=\mathrm{2e}^{\mathrm{2}} \:+\mathrm{2e}^{−\mathrm{2}} \:−\mathrm{4} \\ $$
