Question Number 61801 by aliesam last updated on 08/Jun/19
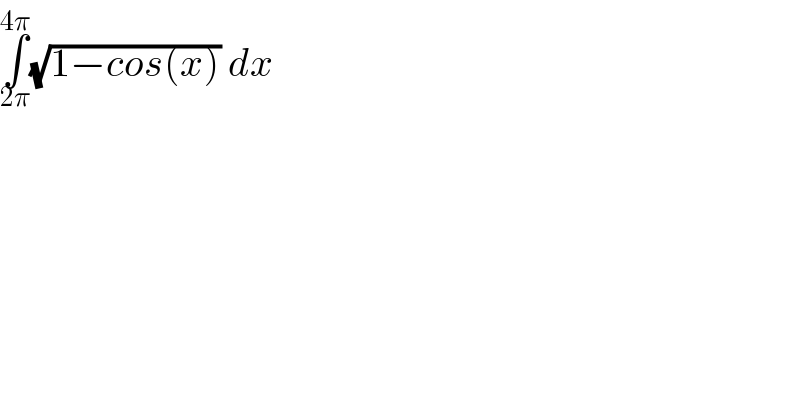
$$\underset{\mathrm{2}\pi} {\overset{\mathrm{4}\pi} {\int}}\sqrt{\mathrm{1}−{cos}\left({x}\right)}\:{dx} \\ $$
Commented by MJS last updated on 08/Jun/19
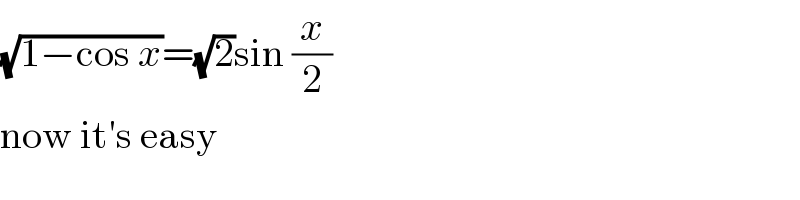
$$\sqrt{\mathrm{1}−\mathrm{cos}\:{x}}=\sqrt{\mathrm{2}}\mathrm{sin}\:\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy} \\ $$
Commented by maxmathsup by imad last updated on 09/Jun/19
![let A =∫_(2π) ^(4π) (√(1−cosx))dx cha7gement x =2π +t give A =∫_0 ^(2π) (√(1−cost))dt =∫_0 ^(2π) (√(2sin^2 ((t/2))))dt =(√2)∫_0 ^(2π) ∣sin((t/2))∣dt 0≤(t/2)≤π ⇒sin((t/2))≥0 ⇒A =(√2)∫_0 ^(2π) sin((t/2)) =(√2)[−2cos((t/2))]_0 ^(2π) =−2(√2){ cos(π)−cos(0)} =−2(√2)(−2) =4(√2) A =4(√2).](https://www.tinkutara.com/question/Q61830.png)
$${let}\:{A}\:=\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \sqrt{\mathrm{1}−{cosx}}{dx}\:\:{cha}\mathrm{7}{gement}\:{x}\:=\mathrm{2}\pi\:+{t}\:{give} \\ $$$${A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{\mathrm{1}−{cost}}{dt}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)}{dt}\:=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid{sin}\left(\frac{{t}}{\mathrm{2}}\right)\mid{dt} \\ $$$$\mathrm{0}\leqslant\frac{{t}}{\mathrm{2}}\leqslant\pi\:\Rightarrow{sin}\left(\frac{{t}}{\mathrm{2}}\right)\geqslant\mathrm{0}\:\Rightarrow{A}\:=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{sin}\left(\frac{{t}}{\mathrm{2}}\right)\:=\sqrt{\mathrm{2}}\left[−\mathrm{2}{cos}\left(\frac{{t}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$=−\mathrm{2}\sqrt{\mathrm{2}}\left\{\:{cos}\left(\pi\right)−{cos}\left(\mathrm{0}\right)\right\}\:=−\mathrm{2}\sqrt{\mathrm{2}}\left(−\mathrm{2}\right)\:=\mathrm{4}\sqrt{\mathrm{2}} \\ $$$${A}\:=\mathrm{4}\sqrt{\mathrm{2}}. \\ $$
Commented by aliesam last updated on 09/Jun/19

$${thanks}\:{sir}\: \\ $$
