Question Number 128182 by BHOOPENDRA last updated on 05/Jan/21

Commented by BHOOPENDRA last updated on 05/Jan/21
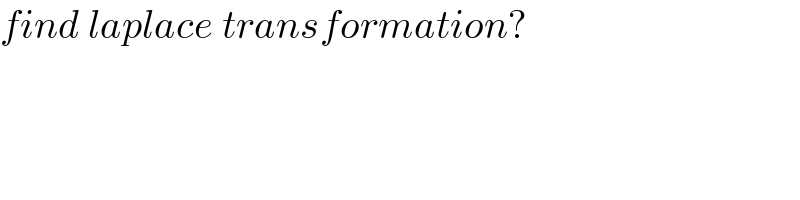
$${find}\:{laplace}\:{transformation}? \\ $$
Answered by mathmax by abdo last updated on 05/Jan/21
![2) { ((f(t)=(t−2)^2 if t>2)),((o if t<2 ⇒L(f(t)) =∫_0 ^∞ e^(−tx) (x−2)^2 dx)) :} =∫_2 ^(+∞) (x−2)^2 e^(−tx) dx =[−(1/t)e^(−tx) (x−2)^2 ]_(x=2) ^∞ +2∫_2 ^(+∞) (1/t)e^(−tx) (x−2)dx =(2/t)∫_2 ^(+∞) e^(−tx) (x−2)dx =(2/t){ [−(1/t)e^(−tx) (x−2)]_2 ^∞ +∫_2 ^∞ (1/t)e^(−tx) dx} =(2/t^2 )∫_2 ^(+∞) e^(−tx) dx =(2/t^2 )[−(1/t)e^(−tx) ]_2 ^∞ =(2/t^2 )((e^(−2t) /t)) =((2e^(−2t) )/t^3 )](https://www.tinkutara.com/question/Q128261.png)
$$\left.\mathrm{2}\right)\begin{cases}{\mathrm{f}\left(\mathrm{t}\right)=\left(\mathrm{t}−\mathrm{2}\right)^{\mathrm{2}} \:\mathrm{if}\:\mathrm{t}>\mathrm{2}}\\{\mathrm{o}\:\mathrm{if}\:\mathrm{t}<\mathrm{2}\:\Rightarrow\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{tx}} \left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \mathrm{dx}}\end{cases} \\ $$$$=\int_{\mathrm{2}} ^{+\infty} \:\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{tx}} \:\mathrm{dx}\:=\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{e}^{−\mathrm{tx}} \:\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \right]_{\mathrm{x}=\mathrm{2}} ^{\infty} +\mathrm{2}\int_{\mathrm{2}} ^{+\infty} \frac{\mathrm{1}}{\mathrm{t}}\mathrm{e}^{−\mathrm{tx}} \left(\mathrm{x}−\mathrm{2}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{t}}\int_{\mathrm{2}} ^{+\infty} \:\mathrm{e}^{−\mathrm{tx}} \left(\mathrm{x}−\mathrm{2}\right)\mathrm{dx}\: \\ $$$$=\frac{\mathrm{2}}{\mathrm{t}}\left\{\:\:\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{e}^{−\mathrm{tx}} \:\left(\mathrm{x}−\mathrm{2}\right)\right]_{\mathrm{2}} ^{\infty} +\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{t}}\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }\int_{\mathrm{2}} ^{+\infty} \:\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:=\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{e}^{−\mathrm{tx}} \right]_{\mathrm{2}} ^{\infty} \\ $$$$=\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }\left(\frac{\mathrm{e}^{−\mathrm{2t}} }{\mathrm{t}}\right)\:=\frac{\mathrm{2e}^{−\mathrm{2t}} }{\mathrm{t}^{\mathrm{3}} } \\ $$$$ \\ $$
Commented by BHOOPENDRA last updated on 06/Jan/21
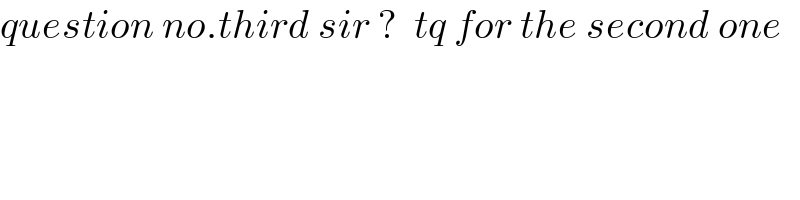
$${question}\:{no}.{third}\:{sir}\:?\:\:{tq}\:{for}\:{the}\:{second}\:{one} \\ $$
