Question Number 65235 by ajfour last updated on 26/Jul/19

Commented by ajfour last updated on 26/Jul/19

$${Find}\:{p},{q},{r}\:{in}\:{terms}\:{of}\:{a},{b},{c}. \\ $$
Commented by ajfour last updated on 27/Jul/19

$${do}\:{explain}\:{a}\:{bit}\:{sir}!\:{thanks}. \\ $$
Answered by mr W last updated on 27/Jul/19

Commented by ajfour last updated on 27/Jul/19
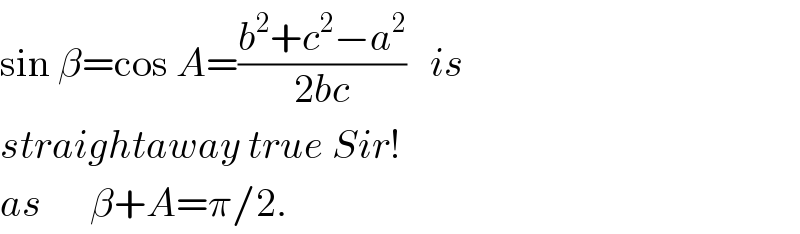
$$\mathrm{sin}\:\beta=\mathrm{cos}\:{A}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\:\:\:{is} \\ $$$${straightaway}\:{true}\:{Sir}! \\ $$$${as}\:\:\:\:\:\:\beta+{A}=\pi/\mathrm{2}. \\ $$
Commented by mr W last updated on 27/Jul/19
![R=radius of circumcircle sin β=((AB′)/(AB)) with BB′⊥AC AB′=((b^2 +c^2 −a^2 )/(2b)) (∗ see below) ⇒sin β=((b^2 +c^2 −a^2 )/(2bc)) sin γ=((AC′)/(AC)) with CC′⊥AB AC′=((c^2 +b^2 −a^2 )/(2c)) ⇒sin γ=((b^2 +c^2 −a^2 )/(2bc))=sin β ⇒β=γ i.e. A is midpoint of QR^(⌢) and OA⊥QR. ∠AOQ=2β p=2R sin 2β=4R sin β cos β sin β=((b^2 +c^2 −a^2 )/(2bc)) cos β=((√((2bc)^2 −(b^2 +c^2 −a^2 )^2 ))/(2bc)) =((√((2bc+b^2 +c^2 −a^2 )(2bc−b^2 −c^2 +a^2 )))/(2bc)) =((√([(b+c)^2 −a^2 ][a^2 −(b−c)^2 ]))/(2bc)) =((√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))/(2bc)) =(a/2)×((√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))/(abc)) =(a/2)×(1/R) p=4R sin β cos β =4R×((b^2 +c^2 −a^2 )/(2bc))×(a/2)×(1/R) ⇒p=((a(b^2 +c^2 −a^2 ))/(bc)) similarly ⇒q=((b(c^2 +a^2 −b^2 ))/(ca)) ⇒r=((c(a^2 +b^2 −c^2 ))/(ab)) (∗) BB′^2 =c^2 −AB′^2 =a^2 −(b−AB′)^2 ⇒c^2 −AB′^2 =a^2 −b^2 −AB′^2 +2bAB′ ⇒b^2 +c^2 −a^2 =2bAB′ ⇒AB′=((b^2 +c^2 −a^2 )/(2b))](https://www.tinkutara.com/question/Q65264.png)
$${R}={radius}\:{of}\:{circumcircle} \\ $$$$\mathrm{sin}\:\beta=\frac{{AB}'}{{AB}}\:{with}\:{BB}'\bot{AC} \\ $$$${AB}'=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{b}}\:\:\:\:\:\:\:\:\:\:\:\left(\ast\:{see}\:{below}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}} \\ $$$$\mathrm{sin}\:\gamma=\frac{{AC}'}{{AC}}\:{with}\:{CC}'\bot{AB} \\ $$$${AC}'=\frac{{c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{c}} \\ $$$$\Rightarrow\mathrm{sin}\:\gamma=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}=\mathrm{sin}\:\beta \\ $$$$\Rightarrow\beta=\gamma \\ $$$${i}.{e}.\:{A}\:{is}\:{midpoint}\:{of}\:\overset{\frown} {{QR}}\:{and}\:{OA}\bot{QR}. \\ $$$$ \\ $$$$\angle{AOQ}=\mathrm{2}\beta \\ $$$${p}=\mathrm{2}{R}\:\mathrm{sin}\:\mathrm{2}\beta=\mathrm{4}{R}\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta \\ $$$$\mathrm{sin}\:\beta=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}} \\ $$$$\mathrm{cos}\:\beta=\frac{\sqrt{\left(\mathrm{2}{bc}\right)^{\mathrm{2}} −\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}{bc}} \\ $$$$=\frac{\sqrt{\left(\mathrm{2}{bc}+{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left(\mathrm{2}{bc}−{b}^{\mathrm{2}} −{c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}}{\mathrm{2}{bc}} \\ $$$$=\frac{\sqrt{\left[\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right]\left[{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right]}}{\mathrm{2}{bc}} \\ $$$$=\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{2}{bc}} \\ $$$$=\frac{{a}}{\mathrm{2}}×\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{{abc}} \\ $$$$=\frac{{a}}{\mathrm{2}}×\frac{\mathrm{1}}{{R}} \\ $$$$ \\ $$$${p}=\mathrm{4}{R}\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta \\ $$$$=\mathrm{4}{R}×\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}×\frac{{a}}{\mathrm{2}}×\frac{\mathrm{1}}{{R}} \\ $$$$\Rightarrow{p}=\frac{{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{{bc}} \\ $$$${similarly} \\ $$$$\Rightarrow{q}=\frac{{b}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{ca}} \\ $$$$\Rightarrow{r}=\frac{{c}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{{ab}} \\ $$$$ \\ $$$$\left(\ast\right) \\ $$$${BB}'^{\mathrm{2}} ={c}^{\mathrm{2}} −{AB}'^{\mathrm{2}} ={a}^{\mathrm{2}} −\left({b}−{AB}'\right)^{\mathrm{2}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} −{AB}'^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{AB}'^{\mathrm{2}} +\mathrm{2}{bAB}' \\ $$$$\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{2}{bAB}' \\ $$$$\Rightarrow{AB}'=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{b}} \\ $$
Commented by mr W last updated on 27/Jul/19

$${thanks}\:{sir}!\:{indeed}\:{much}\:{could}\:{be} \\ $$$${simplified}. \\ $$
Commented by ajfour last updated on 27/Jul/19

$${And}\:\mathrm{cos}\:\beta=\mathrm{sin}\:{A} \\ $$$${and}\:{since}\:\:\frac{\mathrm{sin}\:{A}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$$\:\:\:\:\:\mathrm{cos}\:\beta=\frac{{a}}{\mathrm{2}{R}} \\ $$$${hence}\:\:{p}=\mathrm{2}{R}\mathrm{sin}\:\mathrm{2}\beta \\ $$$$\:\:\:{p}=\mathrm{4}{R}\left(\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\right)\left(\frac{{a}}{\mathrm{2}{R}}\right) \\ $$$$\Rightarrow\:\:{p}=\frac{{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{{bc}}\:. \\ $$$${brilliant}\:{Sir}\:{and}\:{it}'{s}\:{all}\:{quite} \\ $$$${easy}\:{and}\:{straight},\:{then}. \\ $$$$\mathcal{T}{hanks}. \\ $$
