Question Number 8132 by 314159 last updated on 01/Oct/16
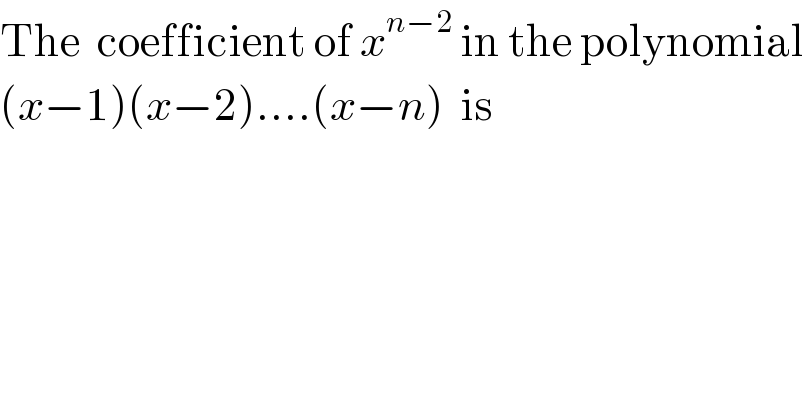
$$\mathrm{The}\:\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{n}−\mathrm{2}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{polynomial} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)….\left({x}−{n}\right)\:\:\mathrm{is} \\ $$
Commented by Yozzia last updated on 01/Oct/16
![coefficient(x^(n−2) )=Σ_(∀α,β∈[1,n]) αβ 1×2+1×3+1×4+...+1×n +2×3+2×4+2×5+...+2×n +3×4+3×5+...+3+n +...+(n−1)×n](https://www.tinkutara.com/question/Q8133.png)
$${coefficient}\left({x}^{{n}−\mathrm{2}} \right)=\underset{\forall\alpha,\beta\in\left[\mathrm{1},{n}\right]} {\sum}\alpha\beta \\ $$$$\mathrm{1}×\mathrm{2}+\mathrm{1}×\mathrm{3}+\mathrm{1}×\mathrm{4}+…+\mathrm{1}×{n} \\ $$$$+\mathrm{2}×\mathrm{3}+\mathrm{2}×\mathrm{4}+\mathrm{2}×\mathrm{5}+…+\mathrm{2}×{n} \\ $$$$+\mathrm{3}×\mathrm{4}+\mathrm{3}×\mathrm{5}+…+\mathrm{3}+{n} \\ $$$$+…+\left({n}−\mathrm{1}\right)×{n} \\ $$$$ \\ $$$$ \\ $$
Answered by prakash jain last updated on 01/Oct/16

$$\mathrm{From}\:\mathrm{Yozzi}'\mathrm{s}\:\mathrm{comment} \\ $$$$\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\:\underset{{i}={j}+\mathrm{1}} {\overset{{n}} {\sum}}{j}\centerdot{i} \\ $$$$\mathrm{Please}\:\mathrm{see}\:\mathrm{post}\:\mathrm{from}\:\mathrm{sou}\:{Q}\mathrm{8139}\:\mathrm{for}\:\mathrm{correct}\:\mathrm{answer}. \\ $$
Commented by prakash jain last updated on 02/Oct/16
![Σ_(j=1) ^(n−1) j(Σ_(i=1) ^n i−Σ_(i=1) ^j j) =Σ_(j=1) ^(n−1) j((n(n+1))/2)−Σ_(j=1) ^(n−1) j((j(j+1))/2) =((n(n+1)n(n−1))/4)−Σ_(j=1) ^(n−1) ((j^3 +j^2 )/2) =((n^2 (n−1)(n+1))/4)−(1/2){(((n−1)n)/2)}^2 −(1/2){(((n−1)n(2n−1))/6)} =((n(n−1))/(24))[6n(n+1)−3n(n−1)−2(2n−1)] =((n(n−1))/(24))[6n^2 +6n−3n^2 +3n−4n+2] =((n(n−1))/(24))[3n^2 +5n+2] =((n(n−1))/(24))[3n^2 +3n+2n+2] =((n(n−1)(n+1)(3n+2))/(24))](https://www.tinkutara.com/question/Q8141.png)
$$\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{j}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}−\underset{{i}=\mathrm{1}} {\overset{{j}} {\sum}}{j}\right) \\ $$$$=\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{j}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{j}\frac{{j}\left({j}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{1}\right)}{\mathrm{4}}−\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{j}^{\mathrm{3}} +{j}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{{n}^{\mathrm{2}} \left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}\right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\left({n}−\mathrm{1}\right){n}\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}\right\} \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{24}}\left[\mathrm{6}{n}\left({n}+\mathrm{1}\right)−\mathrm{3}{n}\left({n}−\mathrm{1}\right)−\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)\right] \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{24}}\left[\mathrm{6}{n}^{\mathrm{2}} +\mathrm{6}{n}−\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{4}{n}+\mathrm{2}\right] \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{24}}\left[\mathrm{3}{n}^{\mathrm{2}} +\mathrm{5}{n}+\mathrm{2}\right] \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{24}}\left[\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}{n}+\mathrm{2}\right] \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}{\mathrm{24}} \\ $$
