Question Number 53277 by 0955083339 last updated on 19/Jan/19
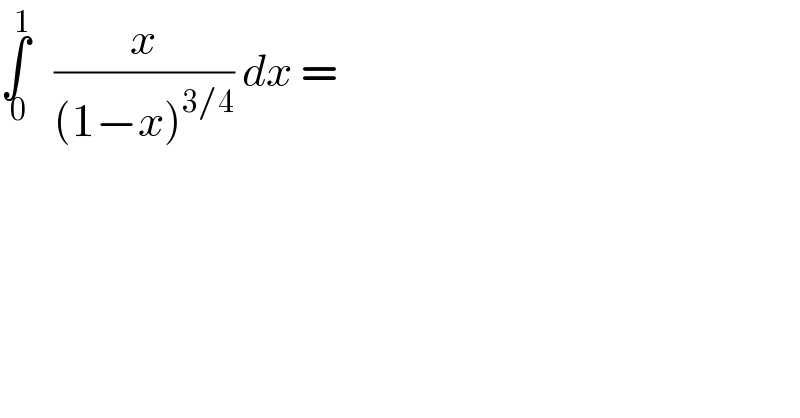
$$\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{4}} }\:{dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 19/Jan/19
![let I =∫_0 ^1 (x/((1−x)^(3/4) ))dx cha7gement 1−x=t give I =∫_0 ^1 ((1−t)/t^(3/4) ) dt =∫_0 ^1 t^(−(3/4)) dt −∫_0 ^1 t^(1/4) dt =[(1/(−(3/4)+1))t^(−(3/4)+1) ]_0 ^1 −[(1/((1/4)+1))t^((1/4)+1) ]_0 ^1 =4−(4/5) =((16)/5) .](https://www.tinkutara.com/question/Q53283.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }{dx}\:{cha}\mathrm{7}{gement}\:\mathrm{1}−{x}={t}\:{give}\: \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{t}}{{t}^{\frac{\mathrm{3}}{\mathrm{4}}} }\:{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{−\frac{\mathrm{3}}{\mathrm{4}}} {dt}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{\frac{\mathrm{1}}{\mathrm{4}}} {dt}\: \\ $$$$=\left[\frac{\mathrm{1}}{−\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1}}{t}^{−\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\left[\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}}{t}^{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{4}−\frac{\mathrm{4}}{\mathrm{5}}\:=\frac{\mathrm{16}}{\mathrm{5}}\:. \\ $$
Answered by ajfour last updated on 19/Jan/19

$${let}\:\:\:\:\:{t}^{\mathrm{4}} =\mathrm{1}−{x}\:\:\Rightarrow\:\mathrm{4}{t}^{\mathrm{3}} {dt}\:=\:−{dx} \\ $$$$\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{4}} }\:{dx}\:=\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}−{t}^{\mathrm{4}} }{{t}^{\mathrm{3}} }\:{dx} \\ $$$$\:\:=\:\mathrm{4}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{4}} \right){dt}\:=\:\mathrm{4}−\frac{\mathrm{4}}{\mathrm{5}}\:=\:\frac{\mathrm{16}}{\mathrm{5}}\:. \\ $$
